La distribuzione unitaria e la distribuzione di frequenze sono due concetti fondamentali in statistica, ma capirli è più semplice di quanto pensi! Per fartelo vedere in modo chiaro e immediato, faremo un piccolo esempio pratico.
Se vuoi approfondire meglio l’argomento, nel nostro canale YouTube troverai un video dedicato, che puoi guardare anche alla fine di questo post. Non perdere l’occasione di rendere la statistica più semplice e intuitiva!
ESEMPIO PRATICO:
Immagina di osservare una classe composta da dieci studenti: questo sarà il nostro collettivo, o meglio, la nostra popolazione di riferimento. Da qui, possiamo analizzare i dati in due modi diversi: considerando ogni singolo valore osservato (distribuzione unitaria) o raggruppandoli per frequenza (distribuzione di frequenze).
Distribuzione unitaria semplice
Iniziamo con l’osservare soltanto l’altezza (il carattere, o caratteristica) dei nostri 10 studenti.
Riportiamo i dati osservati nella seguente tabella statistica:
| Nome | Altezza (in cm) |
| Francesca | 164 |
| Giorgio | 177 |
| Laura | 166 |
| Pietro | 178 |
| Filippo | 182 |
| Ada | 158 |
| Giovanna | 169 |
| Luca | 172 |
| Rossana | 165 |
| Mario | 174 |
Quella che vediamo è una distribuzione unitaria semplice.
La distribuzione unitaria semplice consiste semplicemente nel fare una lista delle modalità assunte, unità per unità, dai componenti del collettivo osservato.
*Le modalità sono i valori che il carattere può assumere. Nel nostro esempio sono le altezze espresse in centimetri.
Abbiamo visto che la distribuzione unitaria semplice, è davvero semplice. Nomen omen.
Adesso, proviamo ad aggiungere un po’ di complessità, inserendo altre caratteristiche osservate nei nostri alunni. In particolare il loro peso, e il colore dei loro occhi.
Questo ci aiuterà ad illustrare la distribuzione unitaria multipla.
Distribuzione unitaria multipla
Ecco l’elenco degli stessi alunni, al quale aggiungiamo, oltre all’altezza, anche il peso e il colore degli occhi:
| Nome | Altezza (in cm) | Peso (in kg) | Colore degli occhi |
| Francesca | 164 | 47,5 | Blu |
| Giorgio | 177 | 69,4 | Marroni |
| Laura | 166 | 49 | Verdi |
| Pietro | 178 | 70 | Marroni |
| Filippo | 182 | 74 | Marroni |
| Ada | 158 | 40,3 | Blu |
| Giovanna | 169 | 48,9 | Verdi |
| Luca | 172 | 66,8 | Marroni |
| Rossana | 165 | 50,1 | Verdi |
| Mario | 174 | 72,7 | Verdi |
La distribuzione unitaria multipla, è come la distribuzione unitaria semplice, con l’unica differenza che i caratteri osservati sono più di uno.
Prima osservavamo soltanto l’altezza (in centimetri), mentre qui abbiamo inserito altri caratteri osservati (il peso ed il colore degli occhi), e dunque osserviamo in totale tre caratteri, unità per unità (per questo si dice distribuzione unitaria).
Distribuzione di frequenze
Adesso osserviamo soltanto il colore degli occhi dei dieci alunni. Abbiamo visto che alcuni hanno gli occhi blu, altri marroni, altri ancora verdi.
Quanto di frequente gli alunni hanno gli occhi blu? E marroni? E verdi?
Per rispondere a questa domanda possiamo contare quanti alunni hanno gli occhi blu, quanti marroni e quanti verdi.
Scrivendo in una tabella le diverse modalità del carattere “Colore degli occhi” (Blu, Marroni, Verdi), e scrivendo accanto alla modalità quante volte questa viene osservata, otteniamo una distribuzione di frequenze, come quella qui sotto.
| Colore degli occhi | Frequenza assoluta |
| Blu | 2 |
| Marroni | 4 |
| Verdi | 4 |
| TOTALE | 10 |
Sappiamo che soltanto Francesca e Ada hanno gli occhi blu, quindi la frequenza è due, e facciamo la stessa cosa contando quanti alunni hanno gli occhi marroni, e quanti verdi.
Il totale è il numero di osservazioni effettuate (ovvero il numero di studenti della classe, dieci).
La distribuzione di frequenza è una tabella in cui indichiamo le modalità di un carattere, e la frequenza con il quale questa modalità viene osservata.
Notiamo che queste sono le frequenze assolute. Ovvero queste frequenze ci dicono in assoluto quanti alunni hanno gli occhi blu, quanti marroni, e quanti verdi.
Può essere utile talvolta rappresentare le frequenze relative, e le frequenze percentuali.
Rappresentazione formale della distribuzione di frequenze
In molti testi, la distribuzione di frequenze è rappresentata formalmente con una tabella come questa:
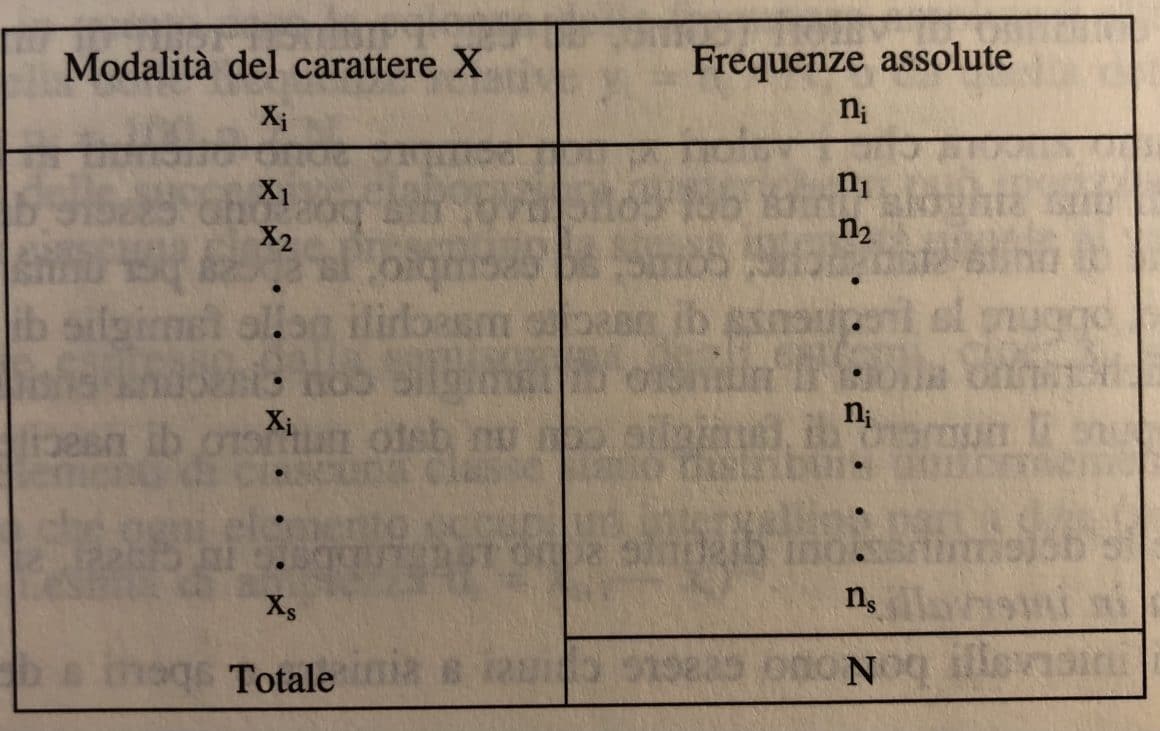
Nella colonna di sinistra, abbiamo le diverse modalità assunte dal carattere.
Nel nostro esempio precedente sul colore degli occhi, queste modalità erano “Blu”, “Marrone” e “Verde”.
Nella colonna di destra, invece, vediamo le frequenze assolute, ovvero quanto di frequente ciascuna modalità viene osservata.
Riferendoci sempre al nostro esempio precedente, a destra vedremo quanti alunni hanno gli occhi blu, quanti marroni, e quanti verdi.
Un esempio di distribuzione di frequenze
Vediamo di seguito un semplice esempio di distribuzione di frequenze, in cui vengono riportate le frequenze assolute delle famiglie italiane, in base al numero di componenti.
P.S. In questo caso, il “Numero di componenti” o “Ampiezza” è il carattere osservato.
Le modalità del carattere sono 1, 2, 3, 4, 5, 6, 7 e più.

In questa distribuzione di frequenze, vediamo che nel 1991, in Italia, c’erano 4.100 famiglie di un componente, 4.920 famiglie di due componenti, 4.411 famiglie di tre componenti, e così via.
Le famiglie prese in considerazione in totale, sono 19.909.
Video sulle distribuzioni unitarie e di frequenze
Domande e risposte sulle distribuzioni unitarie e di frequenze
È semplicemente una lista dei valori osservati, unità per unità.
Ad esempio, se osservassimo le altezze in centrimetri dei componenti di una classe, la distribuzione unitaria semplice, sarebbe la seguente:
162
158
171
174
183
168
162
171
174
171
È un modo di rappresentare dei dati osservati su un collettivo.
Mostra le modalità assunte da un carattere, e la frequenza con cui ciascuna modalità viene osservata.
Facci sapere cosa ne pensi di questo post lasciando la tua valutazione qui sotto!




