Questo post tratta delle imprese e della produzione in microeconomia.
Per comprendere appieno a questo post è possibile che sia necessaria la conoscenza di altri argomenti di microeconomia.
Se fosse questo il tuo caso, puoi visitare la pagina dedicata alla microeconomia cliccando sul pulsante qui sotto:
L’obiettivo di massimizzazione del profitto
Quando si analizza la produzione in microeconomia si trascurano le complicazioni che potrebbero sorgere se i proprietari delle imprese fossero diversi da chi le gestisce: i manager (disallineamento degli obiettivi).
Si ipotizza che il proprietario sia anche colui che gestisce l’impresa.
PROPRIETARIO = MANAGER
Gli obiettivi dei proprietari sono molteplici. Nell’analisi del comportamento delle imprese ci concentriamo esclusivamente sull’obiettivo della massimizzazione del profitto.
Per convenzione il profitto si indica con la lettera greca “pi” (π).
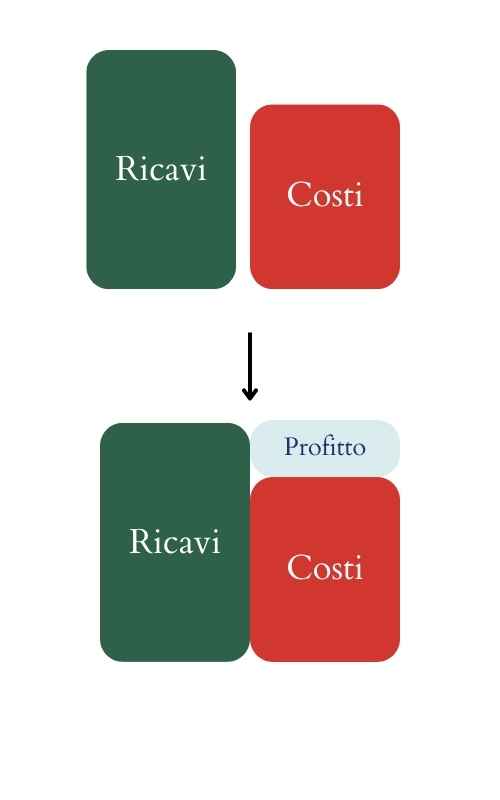
π = R – C
Dove R sono i Ricavi e C i Costi.
Per massimizzare il profitto l’imprenditore deve massimizzare i ricavi e minimizzare i costi.
La produzione in microeconomia: generalità
Per produrre beni/servizio l’impresa utilizza degli input (fattori della produzione).
I fattori della produzione e la funzione di produzione
I fattori della produzione utilizzati sono moltissimi, ma possono essere sintetizzati in tre categorie principali:
- LAVORO – L [Prestazioni occasionali, lavoratori specializzati, lavoratori non specializzati, ecc…]
- CAPITALE – K [indica gli input durevoli come terreni, fabbricati, attrezzature ecc…]
- MATERIE PRIME – M [Indica le materie prime, i semilavorati e i prodotti finiti utilizzati nel processo produttivo].
Per fare un esempio, prendiamo un’impresa che produce pneumatici per auto. Dovrà impiegare delle materie prime (M – come la gomma naturale o sintetica, e l’olio), del capitale (K – come i fabbricati in cui avviare la produzione, gli uffici, le presse per la vulcanizzazione)e del lavoro (L – come gli impiegati della linea di produzione, i venditori, il personale amministrativo).
Dunque in questa ipotetica impresa di produzione di pneumatici, entrano delle materie prime, subiscono una trasformazione (impiegando lavoro e capitale)ed escono fuori dal processo produttivo altri prodotti, i prodotti finiti (nel nostro esempio, i pneumatici).
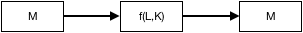
Quella al centro del grafico sovrastante è la funzione di produzione.
La funzione di produzione indica la quantità prodotta, detta output (q)che varia in base ai fattori produttivi (detti input: L, K):
q = f(L,K)
*IPOTESI DI EFFICIENZA: la funzione di produzione in microeconomia contiene soltanto la quantità massima che si può produrre.
Si suppone che non ci siano inefficienze.
Il tempo e la variabilità degli input
Ad ogni impresa occorre del tempo per modificare i fattori di produzione.
Riprendendo l’esempio precedente, un’impresa produttrice di pneumatici ha bisogno di tempo per trovare nuove presse per la vulcanizzazione, operai specializzati per il loro utilizzo, nuovi fornitori, per modificare gli impianti produttivi, e così via.
Riguardo al tempo, lo studio della produzione in microeconomia distingue due lassi temporali:
- BREVE PERIODO: è un lasso di tempo tanto breve da NON consentire l’adeguamento di uno dei fattori produttivi (K o L);
- LUNGO PERIODO: è il lasso di tempo sufficientemente lungo da consentire l’adeguamento di tutti i fattori produttivi (dunque nel lungo periodo tutti gli input sono variabili).

Quindi nel ‘breve periodo’ per definizione si può adeguare un input soltanto alle esigenze della produzione (il lavoro o il capitale).
Nel breve periodo abbiamo un input fisso che non può essere modificato (si indica tipicamente con una linea sopra: K̅ o L̅)e un input variabile.
Solitamente l’input fisso nel breve periodo è il capitale (K̅).
Nel ‘lungo periodo’, per definizione, tutti i fattori della produzione possono essere adeguati, dunque non ci sono input fissi.
Gli input nel lungo periodo sono tutti variabili.
La produzione di breve periodo
UN INPUT VARIABILE E UNO FISSO
Come abbiamo già detto, nel breve periodo uno degli input (tipicamente il capitale, K̅)è fisso.
Dunque lo indicheremo nella funzione di produzione con una barretta sopra (per indicare che quello è l’input fisso):
q = f(L,K̅)
Introduciamo alcuni concetti:
Prodotto totale (q): è la quantità totale prodotta, dati i fattori produttivi
Prodotto marginale del lavoro (MPL) [Marginal Product of Labour].
Indica la variazione di prodotto totale derivante dall’utilizzo di un’unità aggiuntiva di lavoro
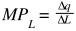
Prodotto medio del lavoro (APL) [Average product of labour]
È il rapporto tra la produzione totale (q)e il lavoro totale (L)impiegato per realizzarlo.
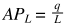
Per vedere in pratica tutti questi concetti, facciamo un esempio sulla funzione di produzione in breve periodo.
Un esempio sulla funzione di produzione di breve periodo
Ipotizziamo che un’azienda abbia 8 postazioni di lavoro (K̅)fisse nel breve periodo, e che la manodopera (L)sia l’input variabile.
In altre parole, l’azienda non può modificare il capitale (K̅, le postazioni di lavoro), ma può modificare la forza lavoro aggiungendo o rimuovendo lavoratori.
Avremo la seguente tabella, che riassume la funzione di produzione (osserviamola per un attimo, prima di commentarla):
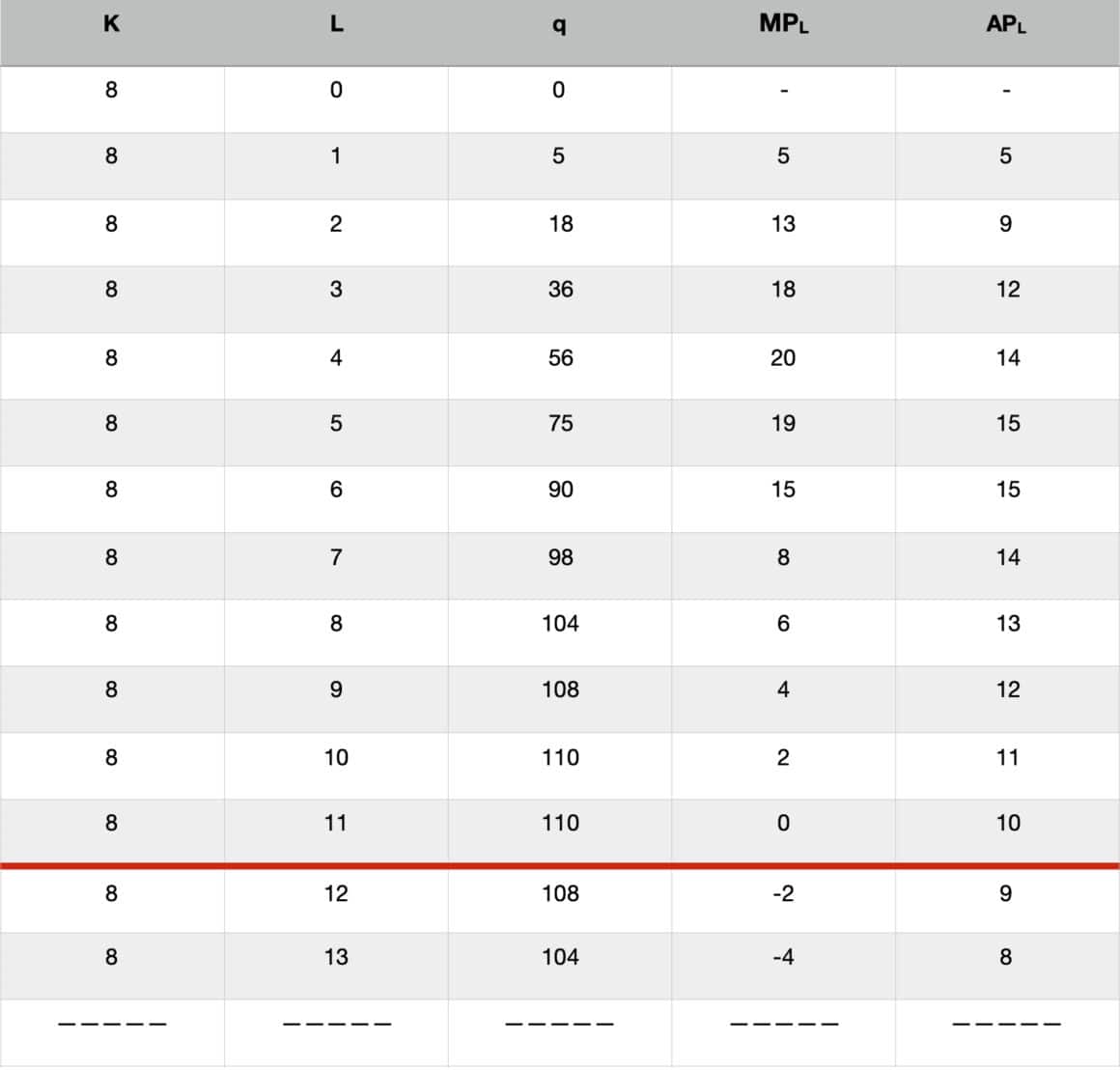
La prima colonna a sinistra è quella del capitale impiegato (K̅)che abbiamo detto essere fisso – in quanto siamo nel breve periodo – ad 8 unità.
La seconda colonna è quella del lavoro (L – che è l’input variabile). Aumenta di un’unità alla volta. Nella prima riga abbiamo 0 unità di lavoro, nella seconda un’unità di lavoro, e così via.
La terza colonna è quella della quantità prodotta (q). Nella prima riga, con 8 unità di capitale e 0 di lavoro, la quantità prodotta è zero. Nella seconda riga (8 unità di capitale e 1 unità di lavoro, la quantità prodotta è 5, e così via.
Notiamo che la quantità totale prodotta aumenta fino a 11 lavoratori (L).
Da L=12 in poi la quantità di output (q)inizia a diminuire.
La quarta colonna indica il prodotto marginale del lavoro (MPL)come definito in precedenza.
MPL aumenta fino a toccare il suo massimo per 4 unità di lavoro (L=4)e dopo diminuisce, fino ad arrivare a zero in corrispondenza di 11 unità lavorative.
Significa che con 4 lavoratori si ha il massimo prodotto aggiuntivo. Il quinto lavoratore apporta comunque una quantità positiva, sebbene inferiore, così come il sesto e così via.
L’undicesimo lavoratore non apporta prodotto marginale (MPL=0). Dal 12esimo lavoratore in poi, ciascun lavoratore aggiuntivo non soltanto non apporta nuova produzione, ma la fa diminuire (MPL è negativo), quindi i lavoratori aggiuntivi non sono inutili, ma addirittura dannosi.
La quantità totale prodotta (q)inizia quindi a diminuire in corrispondenza di MPL=0
La quinta colonna indica il prodotto medio del lavoro (APL)come definito in precedenza.
Dopo la linea rossa, l’impresa smette di produrre e di aggiungere lavoratori (perché ogni lavoratore aggiuntivo fa diminuire la quantità di output (MPL è negativo dopo la linea rossa!).
Perché ad un certo punto con più lavoratori si produce di meno?
Perché ad un aumento dei lavoratori non corrisponde un adeguamento della struttura produttiva. I lavoratori diventano troppi per i tavoli a disposizione per la lavorazione e iniziano ad ostacolarsi tra di loro. Lo vedremo poco più avanti, in merito alla legge dei rendimenti marginali decrescenti.
Rappresentazione grafica della produzione di breve periodo
Quanto abbiamo osservato nella tabella precedente fornisce tutte le informazioni per rappresentare grafica della produzione nel breve periodo.
Nel grafico seguente vediamo come si rappresenta la funzione di produzione in microeconomia, e la relazione che questa ha con la produttività marginale del lavoro.
I valori numerici si riferiscono alla tabella dell’esempio appena fatto, tuttavia la forma delle curve di produzione è uguale anche per altre imprese (ovviamente, con valori differenti).
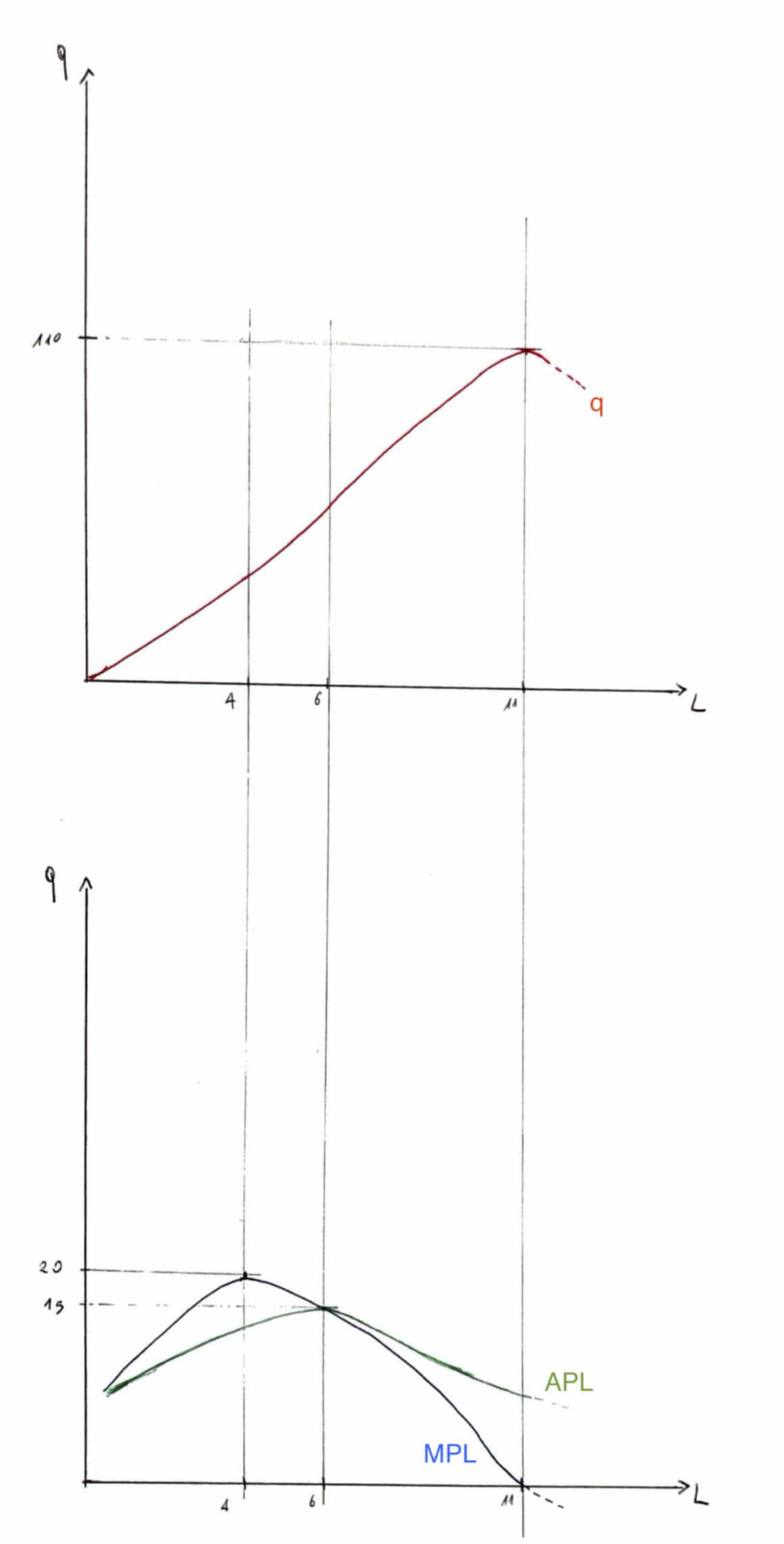
Commentiamo brevemente il grafico.
GRAFICO SUPERIORE: rappresenta la quantità totale prodotta (q – asse delle ordinate)al variare delle unità di lavoro (L – asse delle ascisse, che è l’input variabile nel breve periodo).
GRAFICO INFERIORE: Rappresenta il prodotto marginale del lavoro (MPL) e il prodotto medio del lavoro (APL) nell’asse delle ordinate, al variare delle unità di lavoro (L – asse delle ascisse).
Come vediamo nel grafico superiore, la quantità prodotta (q)tocca il suo massimo in corrispondenza di 11 unità di lavoro (vedi tabella precedente). In particolare, con 11 lavoratori, la quantità prodotta è di 110 unità.
Nel grafico inferiore, in corrispondenza di 11 lavoratori, il prodotto marginale del lavoro (MPL)è zero. Poi comincia a scendere sotto lo zero.
MPL raggiunge il suo massimo (cioè 20)quando ci sono 4 lavoratori.
APL raggiunge il suo massimo quando si interseca con MPL, in corrispondenza di 6 lavoratori.
Notiamo come quando MPL è sopra APL, APL stesso cresce, mentre quando si trova sotto, APL stesso decresce. Questo è logico.
Se la media di quanto prodotto dai lavoratori (APL) è inferiore a quanto ogni lavoratore aggiuntivo produce (MPL), allora il lavoratore aggiuntivo farà salire la media. Viceversa, se la media è maggiore di quanto il lavoratore aggiuntivo produce, il lavoratore aggiuntivo farà diminuire la media.
Dopo 11 unità di lavoro (L), la quantità totale (q)inizia a diminuire, e la quantità prodotta dai lavoratori aggiuntivi (MPL)è inferiore a zero.
Dunque l’impresa non utilizzerà mai più di 11 unità di lavoro (sarebbe controproducente, perché ogni lavoratore aggiuntivo farebbe ridurre l’output totale – q).
L’impresa smette di produrre quando MPL = 0
La legge dei rendimenti marginali decrescenti del lavoro
La legge dei rendimenti marginali decrescenti del lavoro è una legge empirica, che afferma che se un’impresa continua ad aumentare un input (in questo caso il lavoro), mantenendo costanti tutti gli altri input e la tecnologia, i corrispondenti incrementi della quantità prodotta (q)finiranno per diminuire.
In altre parole, se si incrementa un solo input (in questo caso il lavoro – L), il rendimento marginale di tale input finirà per diminuire.
Rendimenti marginali decrescenti è diverso da rendimenti decrescenti.
Il lavoratore aggiuntivo (almeno fin quando MPL non arriva a zero)ha un rendimento marginale decrescente, ma comunque positivo.
Nell’esempio precedente (guarda la tabella sopra)quando MPL iniziava a diminuire (rendimento marginale decrescente), l’impresa continuava comunque a produrre, soltanto che ogni lavoratore aggiuntivo apportava una quantità sempre minore di output (q), fino ad arrivare a zero (MPL = 0).
Ma perché aggiungendo lavoratori, sopra un certo numero, si finisce con l’avere meno quantità prodotta?

Proviamo a comprenderlo con un esempio.
Pensiamo ad un panificio, in cui il capitale è fisso (K̅)ed è costituito da due forni. Il lavoro (L), invece è variabile, ed è costituito dai fornai.
All’inizio ci sono due fornai, e le cose vanno a gonfie vele.
Si pensa di aumentare il fattore lavoro (L)prendendo a lavorare un terzo fornaio, che passa le pagnotte da infornare agli altri due (uno per ciascun forno), e la quantità totale prodotta aumenta.
Allora si assume un quarto fornaio (L = 4), e questo fornaio prepara le pagnotte da passare al secondo fornaio, che le imposta in modo tale che i due addetti ai forni possano infornarle agevolmente. Anche qui la quantità totale prodotta aumenta (q), il che significa che la produttività marginale del lavoro (MPL) è positiva.
Ora immaginiamo che si raggiungano 10 fornai in totale, e ognuno abbia un suo compito e tutto vada per il meglio.
Se si aggiungesse un undicesimo fornaio, la produttività marginale diminuisce ulteriormente, diventando negativa (MPL < 0) perché i vari fornai si intralcerebbero a vicenda, quindi in proprietario del forno deciderà di licenziare l’undicesimo fornaio (mantenerlo significherebbe ridurre la quantità totale prodotta – q).
In altre parole, l’undicesimo fornaio “toglie” più di quanto “aggiunge” perché i fornai sono già abbastanza.
La produzione di lungo periodo
DUE INPUT VARIABILI
Come abbiamo detto, il lungo periodo riguardo alla produzione è per definizione un periodo abbastanza lungo da permettere all’impresa di adeguare i fattori produttivi (K, L)in modo da non avere nessun input fisso.
Nel lungo periodo, tutti gli input sono variabili.
Isoquanti di produzione
L’impresa nel lungo periodo massimizza la quantità prodotta (q)con diverse combinazioni possibili di lavoro (L) e capitale (K).
Tutti gli input sono variabili, quindi l’impresa può scegliere quanto lavoro o capitale usare.
Ad esempio l’impresa può disfarsi dei macchinari inutilizzati, o adeguarli alla produzione necessaria, oppure ancora può trovare operai specializzati.
Dato che tutti gli input sono variabili, l’impresa può scegliere, ad esempio, di produrre la stessa quantità di prodotto usando 1 unità di capitale e 3 di lavoro, oppure 3 unità di capitale e 1 di lavoro (è soltanto un esempio, le proporzioni possono cambiare).
Tutte le combinazioni possibili di lavoro (L)e capitale (K)che danno lo stesso output (q)sono rappresentate dagli isoquanti di produzione.
L’isoquanto indica le combinazioni di input che danno lo stesso output.
(-iso)lo stesso e (-quanto)quantità. La stessa uantità.
Gli isoquanti rappresentano una produzione efficiente.
La rappresentazione grafica degli isoquanti di produzione
Come abbiamo detto, lungo lo stesso isoquanto, la quantità prodotta (q)è la stessa.
Ciò che cambia è la combinazione dei fattori produttivi (K, L).
L’isoquanto è un po’ come la curva di indifferenza per i consumatori.
Vediamolo rappresentato graficamente nella seguente figura:
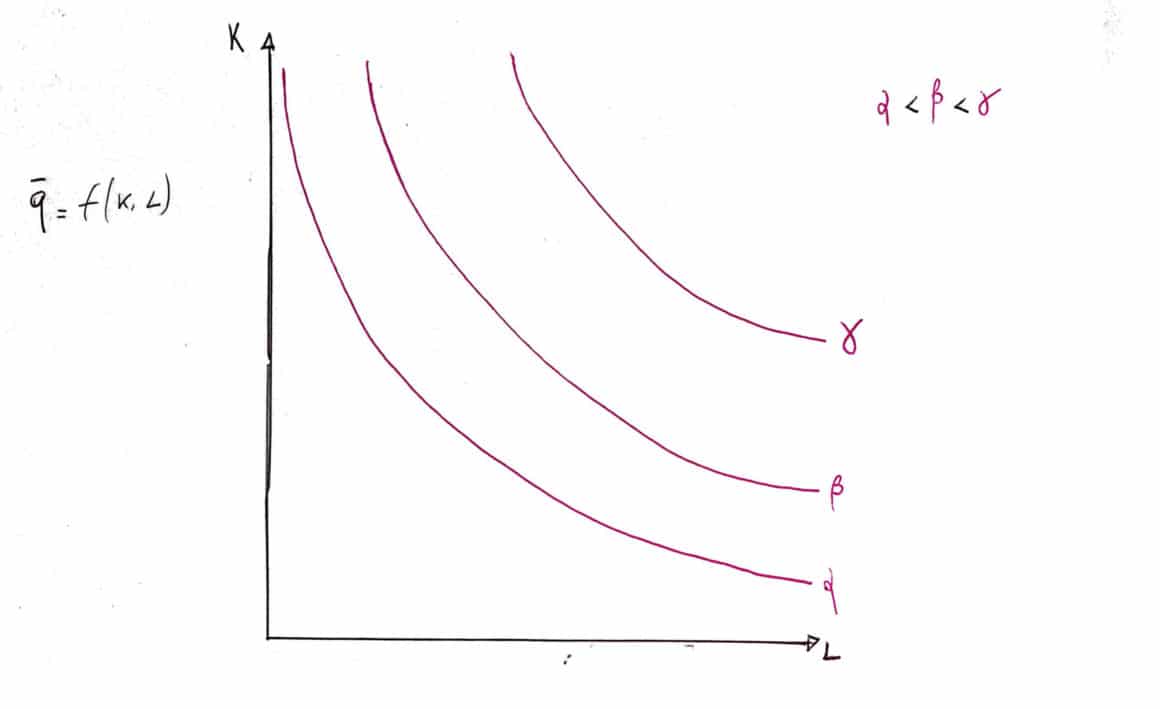
Abbiamo i due input nelle ordinate (K)e nelle ascisse (L), e abbiamo rappresentato tre isoquanti.
Proprietà degli isoquanti
- Più aumenta la distanza dall’origine, maggiore è il livello di produzione ottenuto
- Gli isoquanti non si intersecano tra loro
- Sono convessi rispetto all’origine
- Sono decrescenti.
La pendenza di un isoquanto indica la prontezza con cui un’impresa può sostituire un input con un altro.
Ci sono dei tipi di beni, i qui isoquanti hanno dei grafici particolari. Vediamoli brevemente.
Isoquanti di perfetti sostituti e di input non sostituibili
Gli isoquanti di produzione sono rette con pendenza -1 quando i due input sono perfetti sostituti.
L’impresa può sostituire un input con l’altro liberamente.
È indifferente per l’impresa usare 5 unità di capitale e 1 di lavoro, o viceversa 5 unità di lavoro e una di capitale.
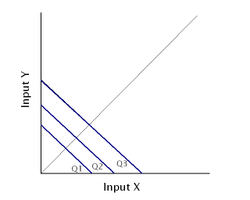
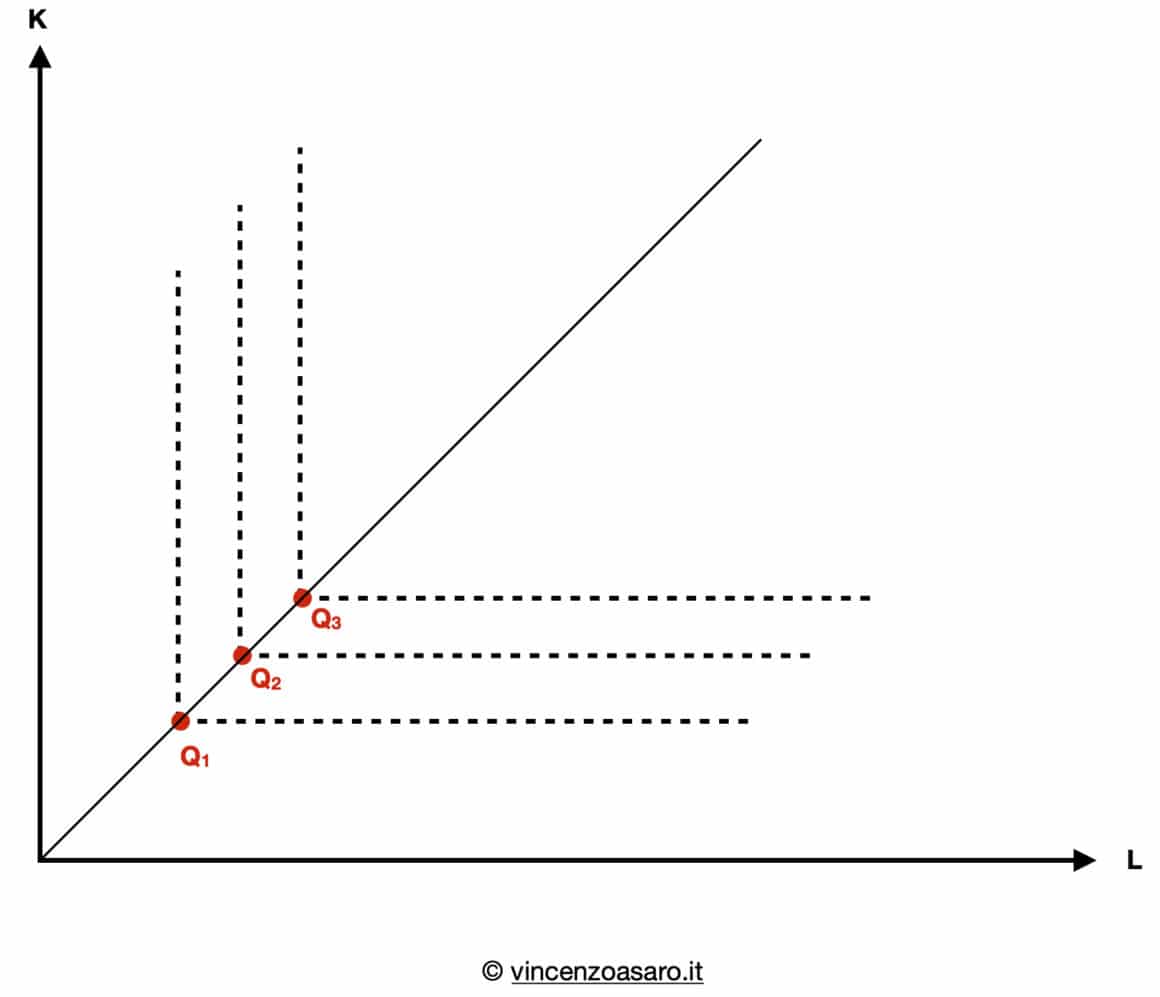
Quando gli input non sono sostituibili (ovvero quando ci vuole la stessa proporzione della combinazione dei due input), l’isoquanto è formato da dei punti (indicati nel grafico con Q1, Q2, Q3, o qualsiasi altro punto che mantenga la stessa proporzione, dunque sulla stessa retta).
La linea tratteggiata fa notare come aggiungendo capitale o lavoro, non ci sarebbe nessuna quantità prodotta quando i due input sono non sostituibili.
Un esempio di input non sostituibili può essere un macchinario (K)che deve essere utilizzato necessariamente da 2 operai (L), non uno di più e non uno di meno.
La sostituzione degli input
La pendenza di un isoquanto di produzione indica la prontezza con cui l’impresa può sostituire un input con un altro, mantenendo costante la quantità prodotta.
Il valore assoluto della pendenza di un isoquanto è chiamato tasso marginale di sostituzione tecnica: MRTS (Marginal Rate of Technical Substitution).
A volte viene indicato anche con l’acronimo italiano SMST (Saggio marginale di sostituzione tecnica).
MRTS indica il numero delle unità di capitale che l’impresa può sostituire con un’unità aggiuntiva di lavoro, mantenendo costante la quantità prodotta (q̅).
Il concetto si esprime con la seguente uguaglianza:
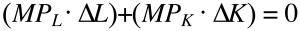
Quest’uguaglianza ha due parti. La prima moltiplica il prodotto marginale del lavoro (MPL)per la variazione di unità di lavoro (∆L). La seconda moltiplica il prodotto marginale del capitale (MPK)per la variazione di unità di capitale impiegate (∆K).
Ovvero quest’uguaglianza ci dice: affinché la variazione di quantità prodotta sia zero (in modo da trovarsi ancora sullo stesso isoquanto), la variazione di produttività dovuta al lavoro (prima parte)deve essere compensata dalla variazione di produttività dovuta al capitale (seconda parte)
Riordinando i termini, otterremo:
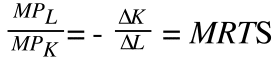
La rappresentazione grafica del saggio marginale di sostituzione tecnica (MRTS)può rendere meglio l’idea:
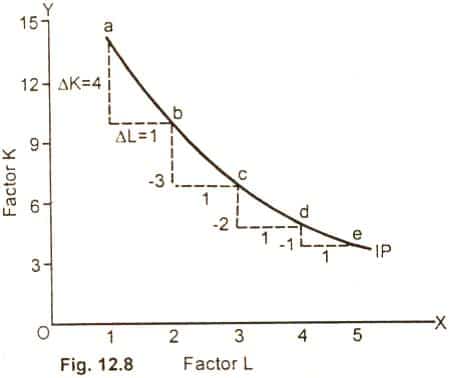
Nel grafico osserviamo che con 1 lavoratore (asse delle ascisse), l’impresa impiega 14 unità di capitale (asse delle ordinate).
Per produrre la stessa quantità (sullo stesso isoquanto)aggiungendo un secondo lavoratore (L=2), l’impresa deve impiegare soltanto 10 unità di capitale (K = 10).
Dunque la variazione di capitale è 4 (∆K = 4).
Quando l’impresa ha 2 lavoratori, aggiungendo un terzo lavoratore (L =3), l’impresa deve impiegare 7 unità di capitale (K = 7)per produrre la stessa quantità. Dunque la variazione di capitale è 3 (∆K = 3).
E così via.
MRTS ci serve anche quando vogliamo calcolare la combinazione ottima dei fattori produttivi.
Infatti, per determinare l’ottima combinazione dei fattori produttivi ci basterà eguagliare MRTS = w/r.
Tutte le informazioni dettagliate sono contenute nel post dedicato all’argomento, al quale potete accedere usando il pulsante qui sotto:
La produzione in microeconomia: i rendimenti di scala
I rendimenti di scala si riferiscono ala variazione di output che segue alla variazione proporzionale di entrambi gli input.
Mi spiego meglio. I rendimenti di scala rispondono alla domanda: se modifico della stessa proporzione (ad esempio del 10%)sia il capitale che il lavoro impiegato, di quanto cambia la produzione totale?
Facciamo un esempio giusto per capirci: ipotizziamo di raddoppiare entrambi i fattori produttivi (L, K)impiegati.
*NOTA: è soltanto un esempio. Il ragionamento varrebbe anche se dimezzassimo i fattori produttivi, o se li decuplicassimo. Lo vedremo a breve.
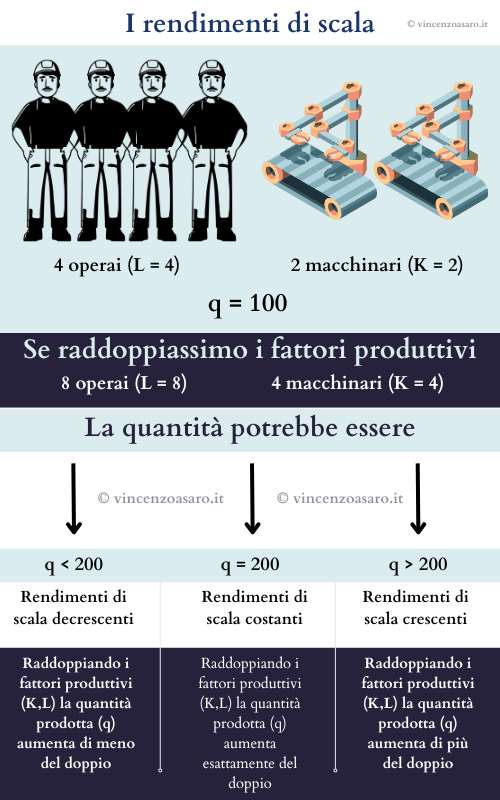
All’inizio, impiego una certa quantità di lavoro e una certa quantità di capitale, e produco una quantità q. Ipotizziamo che q =100.
Raddoppiando i fattori produttivi impiegati (il lavoro e il capitale)possiamo avere tre situazioni:
- q = 200
Abbiamo raddoppiato i fattori produttivi impiegati, dunque la quantità prodotta è raddoppiata.
In questo caso, si parla di rendimenti di scala costanti. - q < 200
Abbiamo raddoppiato i fattori produttivi impiegati, ma la quantità prodotta (q)è inferiore al doppio della precedente.
In questo caso, si parla di rendimenti di scala decrescenti (abbiamo usato il doppio degli input, e la quantità è aumentata di meno del doppio). - q > 200
Abbiamo raddoppiato i fattori produttivi impiegati, e la quantità prodotta (q)è superiore al doppio della precedente.
In questo caso, si parla di rendimenti di scala crescenti (abbiamo usato il doppio degli input, e la quantità è aumentata di più del doppio).
Osserviamo l’immagine sottostante per far sì che rimanga impresso l’esempio appena fatto, e poi proviamo a formalizzare un po’ di più il concetto:
Ricordiamo la funzione di produzione che avevamo introdotto all’inizio in questo post:
q = f(K,L)
La quantità prodotta è funzione del capitale (K)e del lavoro impiegato.
Aumentare entrambi gli input (K,L)proporzionalmente significa moltiplicarli entrambi per un parametro, che chiameremo alfa (α).
Ad esempio, se raddoppiamo entrambi i fattori (K ed L), alfa sarà due (α = 2).
Quindi avremo q = f(αK, αL)
Si possono verificare tre situazioni separate quando si aumentano gli input in maniera proporzionale (moltiplicandoli per un parametro α).
Rendimenti di scala costanti
Aumentando della stessa proporzione gli input (L, K), la quantità prodotta (q)aumenta proporzionalmente.
Ad esempio, raddoppio gli input, raddoppia anche la quantità prodotta.
Quadruplico gli input, quadruplica anche la quantità prodotta.
E così via.
Formalmente, i rendimenti di scala costanti si indicano con la seguente formula:
f(αK, αL) = α * f(K,L)
Al primo membro, abbiamo aumentato entrambi gli input moltiplicandoli per α.
Se per esempio si usavano 3 unità di K e 5 unità di L, e α=2, adesso si usano 6 unità di k, e 10 unità di L.
Al secondo membro, abbiamo moltiplicato la vecchia quantità prodotta (con 3 unità di K e 5 unità di L)per α.
Rendimenti di scala decrescenti
Aumentando della stessa proporzione gli input (L, K), la quantità prodotta (q)aumenta meno che proporzionalmente.
Ad esempio, raddoppio gli input e la quantità prodotta è meno del doppio di prima.
Quadruplico gli input, e la quantità prodotta è meno del quadruplo di quanto producevo prima.
E così via.
Formalmente, i rendimenti di scala decrescenti si indicano con la seguente formula:
f(αK, αL) < α * f(K,L)
Al primo membro, abbiamo la quantità prodotta moltiplicando entrambi gli input per α.
Al secondo membro, abbiamo moltiplicato la quantità prodotta con i vecchi input per α.
Rendimenti di scala crescenti
Aumentando della stessa proporzione gli input (L, K), la quantità prodotta (q)aumenta più che proporzionalmente.
Ad esempio, raddoppio gli input e la quantità prodotta è più del doppio di prima.
Quadruplico gli input, e la quantità prodotta è più del quadruplo di quanto producevo prima.
E così via.
Formalmente, i rendimenti di scala crescenti si indicano con la seguente formula:
f(αK, αL) > α * f(K,L)
Al primo membro, abbiamo la quantità prodotta moltiplicando entrambi gli input per α.
Al secondo membro, abbiamo moltiplicato la quantità prodotta con i vecchi input per α.
Esempio sui rendimenti di scala
Qualora il concetto non dovesse essere ancora chiaro, facciamo un ulteriore esempio sui rendimenti di scala.
Ipotizziamo di avere una funzione di produzione, che in corrispondenza di 5 unità di capitale (K) e 7 unità di lavoro (L), dia un output di 15 unità.
Sarà rappresentata come segue:
f (5, 7) = 15
Adesso ipotizziamo di raddoppiare entrambi gli input (quindi di aumentarli proporzionalmente entrambi del doppio). Avremo:
f(2*5, 2*7) = f(10,14)
Avendo raddoppiato entrambi gli input, quale sarà l’output prodotto in più (ricordando che prima di raddoppiarli producevamo 15 unità)?
- Se f(10,14) = 30 allora i rendimenti di scala saranno costanti (perché l’aumento dell’output, è stato esattamente del doppio (2*15).
- Se f(10,14)>30 (ad esempio 31, o qualsiasi altro numero superiore), allora i rendimenti di scala saranno crescenti.
Raddoppiando entrambi gli input (K,L)l’output è più che raddoppiato! - Infine, nel caso in cui f(10,14)<30 (ad esempio 29, o qualsiasi altro numero superiore), allora i rendimenti di scala saranno decrescenti.
Raddoppiando entrambi gli input (K,L)l’output è meno che raddoppiato!
La produzione in microeconomia e il progresso tecnologico
La produzione in microeconomia è influenzata dal progresso tecnologico.
Le innovazioni introdotte (in senso ampio, intendendo anche innovazioni nei metodi organizzativi)determinano una maggiore produttività.
Possiamo suddividere il progresso tecnico in due grandi sottocategorie:
- Progresso tecnico neutro: si ha un output maggiore, a parità di input.
Questo tipo di progresso tecnico è detto “neutro” perché non implica un cambiamento nelle quantità di lavoro e capitale impiegate. - Progresso tecnico NON neutro: si ha un aumento nella produttività di uno solo degli input.
Questo tipo di progresso tecnico comporta un cambiamento nelle quantità di lavoro e capitale impiegate. NON è neutro come il precedente.
Se per esempio ad un tratto dei macchinari diventano molto più produttivi, l’impresa dovrà modificare il rapporto di lavoro e capitale utilizzato.
Infografica sulle imprese e la produzione in microeconomia

Puoi scaricare l’infografica sulla produzione in microeconomia, oppure visitare il canale YouTube in cui sono presenti diversi video relativi all’argomento cliccando sui pulsanti qui sotto:
