La media aritmetica è un modo semplice per riassumere un insieme di numeri. Si calcola sommando tutti i valori e dividendo il totale per il numero di valori presenti. In poche parole, è il “punto di equilibrio” tra diversi dati.
Scommetto che hai già usato la media senza nemmeno pensarci! Per esempio, quando calcoli il voto medio dei tuoi esami o confronti il costo medio di un affitto nella tua città. Anche nei giornali trovi spesso riferimenti alla media, come:
– “Ambulanze veterinarie azzurre: a Mantova in media due interventi al giorno.”
– “Mutui: a Bergamo chiesti in media 139mila euro.”
Ma la media aritmetica non è solo un numero qualsiasi: ha proprietà interessanti e può aiutarci a interpretare meglio i dati. In questo articolo la analizzeremo più da vicino, scopriremo quando è utile (e quando può essere fuorviante!) e faremo alcuni esempi pratici per chiarire il concetto.
Pronto? Andiamo!
Introduzione alla media aritmetica
La media aritmetica (che indicheremo in questo post con Ma) è un valore di sintesi della distribuzione di un carattere.
In poche parole, quando si ha una distribuzione, la media aritmetica ci dice in un colpo solo, con un numero solo, dove sta il “centro” della distribuzione.
Quando nel linguaggio comune usiamo la parola media, ci riferiamo proprio alla media aritmetica (anche se in statistica ci sono anche altre medie, come la mediana, o la moda).
Per calcolare la media aritmetica dobbiamo fare due cose:
- Sommare tutti i valori osservati
- Dividere la somma per il numero di osservazioni
Capiamo meglio il concetto con un esempio semplicissimo.
Un semplice esempio
Scorri le slide qui sotto per osservare un semplice esempio di come funziona la media aritmetica.
1
Ci sono due amici, Gigi e Andrea.
Gigi ha in tasca 4 €, e Andrea, invece, ha in tasca 10€.
3
Molto semplice!
Sommiamo i 4 € di Gigi e i 10 € di Andrea (totale 14€)e li dividiamo per due (perchè gli amici sono due).
14 € diviso due fa 7 €.
In media, Gigi e Andrea hanno in tasca 7 €.
7 € è la media aritmetica dei soldi che hanno in tasca Gigi e Andrea!
Un altro semplice esempio
Vediamo un altro esempio, leggermente più complesso, per fissare ulteriormente il concetto.
Scorri le slide qui sotto per vedere l’esempio.
1
Chiediamo ad un gruppo di 5 persone qual è il loro reddito annuo.
Riportiamo le risposte in questa tabella:
Definizione di media aritmetica
La “media aritmetica” (Ma)di un insieme di n valori osservati (x1, x2, x3,…, xn) è pari alla somma dei valori osservati divisa per il loro numero.
È semplicemente quello che abbiamo già detto, ma formalmente si esprime così:
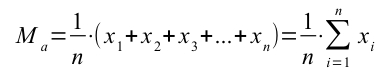
La formula che può sembrare complicata è in realtà molto semplice.
Al numeratore abbiamo la sommatoria di tutti i numeri osservati (sommatoria di xi), e al denominatore abbiamo n (ovvero il numero di osservazioni).
Media di una distribuzione di frequenze
Se il carattere quantitativo X è discreto e conosciamo la distribuzione di frequenze, allora la media sarà rappresentata così:
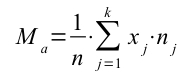
xj indica la modalità del carattere (ad esempio, se osserviamo il reddito di una persona le modalità saranno 1.000 €, 1.500€, ecc…), mentre nj indica la sua frequenza assoluta.
k è il numero delle modalità assunte dal carattere.
Media di una distribuzione con frequenze relative
se anziché le frequenze assolute, usiamo le frequenze relative (fj) la media si rappresenta così:
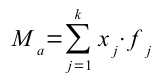
xj indica la modalità del carattere (ad esempio, se osserviamo il reddito di una persona le modalità saranno 1.000 €, 1.500€, ecc…), mentre fj indica la sua frequenza relativa.
In questa formula, come vediamo, non dividiamo per n (perché usiamo le frequenze relative!).
k è il numero delle modalità assunte dal carattere.
Media aritmetica di una distribuzione in classi
Se il carattere è distribuito in classi, il calcolo della media viene fatto in modo diverso. Inoltre, anche il risultato sarà leggermente diverso rispetto al calcolo della media nelle distribuzioni di frequenze (questo perché la distribuzione in classi comporta una certa dose di approssimazione).
Vediamolo subito con un semplice esempio!
Esempio di calcolo della media aritmetica di una distribuzione in classi
Facciamo un’ulteriore esempio, stavolta in modo leggermente più formale.
Ipotizziamo di osservare il numero di cellulari posseduti in una famiglia, questo sarà il nostro carattere X.
X=numero di cellulari posseduti in famiglia.
Costruiamo la distribuzione di frequenze semplice e contemporaneamente una distribuzione con le modalità raggruppate in classi.
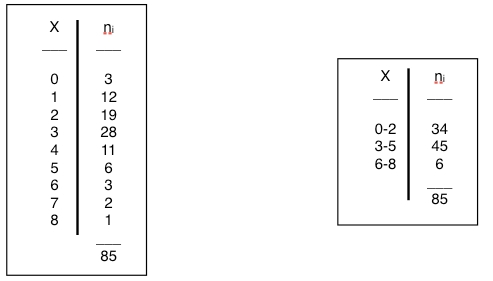
Indicheremo con MaI la media calcolata osservando la distribuzione di frequenze semplice, ovvero usando la formula [2] che vedete sopra.
Indicheremo con MaII la media calcolata osservando la distribuzione di frequenze per classi, quindi come valore di X useremo il valore centrale della classe.
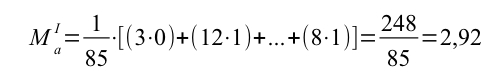
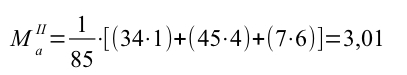
Nella media calcolata sulla distribuzione in classi di frequenza, 1 è il valore medio della prima classe, 4 è il valore medio della seconda classe e 7 è il valore medio della terza classe.
Quindi abbiamo osservato come:
La media aritmetica calcolata su una distribuzione di frequenze, e sulla stessa distribuzione espressa in classi sia diversa.
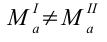
In particolare, nel nostro esempio abbiamo visto che:
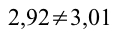
Facciamo anche un’altra osservazione, che seppur ovvia, è opportuno sottolineare:
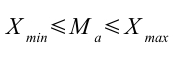
Dove Xmin è la minima modalità assumibile dal carattere, e viceversa Xmax è la massima modalità assumibile dal carattere.
Proviamo a capire quest’ultima osservazione con un esempio semplicissimo: se calcoliamo la media dei voti a scuola, e il voto più basso è 6 (Xmin ) mentre il voto più alto è 10 (Xmax ), è impossibile che la media sia 5, oppure 11. Deve essere compresa tra 6 e 10.
La media ponderata
Cosa succede se ad ogni osservazione vogliamo assegnare un ‘peso’?
Ad esempio, all’università così com’è oggi, ogni materia ha un peso diverso (i crediti formativi).
Nel calcolo della media, una materia da 10 CFU vale di più di una materia da 6 CFU.
In questi casi, si calcola un particolare tipo di media aritmetica, che è detta media ponderata (o anche media pesata).
La indicheremo con pMa .
La pMa(media aritmetica ponderata) di un insieme di n valori x1, x2, x3,…,xn di un carattere quantitativo X, ponderata con i pesi p1, p2, p3,…,pn è data da:
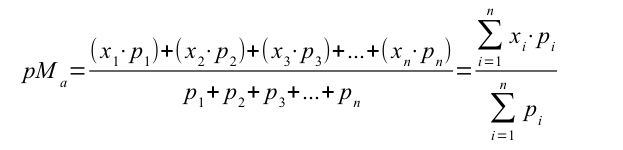
*Osservazione: nella pMa non possono essere usati pesi negativi.
Media ponderata se i pesi sono tutti uguali
Se i pesi sono tutti uguali (ovvero p1 = p2 = p3 =… = pn), allora la media aritmetica sarà uguale alla media ponderata!
pMa = Ma
Dimostriamo questa osservazione:
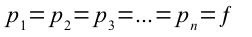
i pesi sono tutti uguali, quindi con f costante abbiamo:
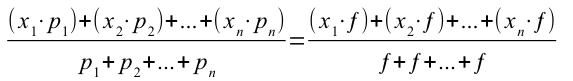
Raggruppando le f al denominatore, e moltiplicando le f per n al denominatore, otteniamo l’equazione qui sotto:
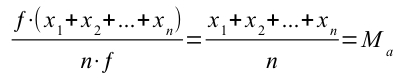
In sostanza abbiamo semplificato le due ƒ al numeratore e al denominatore.
Abbiamo dimostrato come in questo caso (quello in cui i pesi sono tutti uguali), la media ponderata è uguale alla media aritmetica.
Le proprietà della media aritmetica
La Ma presenta alcune importanti proprietà matematiche che elenchiamo di seguito.
Proprietà 1 – La media moltiplicata per il numero di osservazioni (n) è uguale alla somma dei caratteri osservati
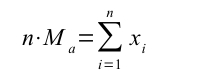
Significa che il numero di osservazioni (n) moltiplicato per la media, è uguale alla somma delle singole osservazioni.
Facciamo un esempio per essere più chiari. Ipotizziamo di osservare la media dei voti nell’esame di statistica, di 6 studenti. I voti sono i seguenti:
| VOTI | 28 | 30 | 28 | 24 | 18 | 22 |
La somma dei voti è 150. Le osservazioni (n)sono sei. Di conseguenza, la media sarà data da 150 diviso 6.
Ma = 25
Se moltiplichiamo 25 per il numero di osservazioni (n=6), otteniamo la somma dei voti di tutti gli alunni (150).
6 x 25 = 150
Proprietà 2 – La sommatoria delle differenze tra i caratteri osservati e la media al quadrato è inferiore o uguale della sommatoria delle differenze tra i caratteri osservati e un’altra costante
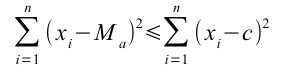
*con c costante e c ≠ Ma
Proprietà 3 – La sommatoria delle differenze tra i caratteri osservati e la media è zero
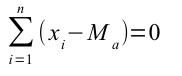
Significa semplicemente che se a ciascuna osservazione sottraessimo la media, il risultato sarebbe zero.
Proprietà 4 – La media è compresa tra il valore minimo e il valore massimo del collettivo preso in considerazione
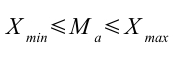
Significa che la media è necessariamente compresa tra il valore minimo osservato (il più basso), e quello massimo (il più alto).
Proprietà 5 – Proprietà associativa della media
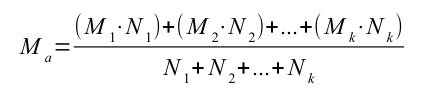
Proprietà associativa della media
Che si può riscrivere come segue:
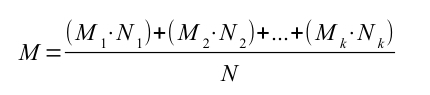
Proprietà associativa della media.
Proprietà 6 – Linearità della media aritmetica
[6] sia X un carattere, con X=(x1, x2, x3,…,xn), la media aritmetica è lineare.
y = ax+b ⇒ My = aMx + b
* Nel caso il punto [6] non sia chiaro rivedere l‘argomento della retta in matematica.
Dimostrazione delle proprietà
Vediamo come dimostrare alcune delle proprietà della media che abbiamo osservato.
Dimostrazione proprietà 1
La proprietà 1 non va dimostrata.
La definizione della media aritmetica è:
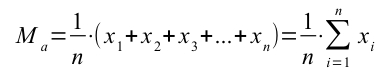
Se moltiplichiamo entrambi i membri per n otteniamo:
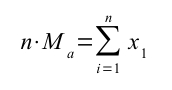
Dimostrazione proprietà 2 e 3
Ricordiamo che la seconda proprietà della media è la seguente:
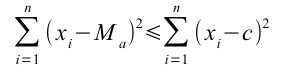
Sappiamo per la proprietà 3 della media che:
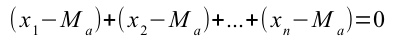
Questo perché:
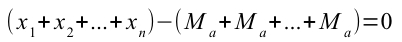
Dunque
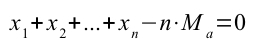
Osserviamo anche che il secondo membro può essere scritto così:
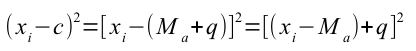
Dunque la sommatoria può essere scritta così:
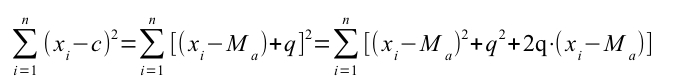
Facendo ulteriori passaggi algebrici, possiamo rappresentare la sommatoria così:
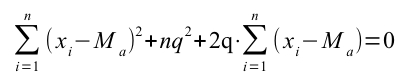
Quindi la sommatoria delle differenze tra i caratteri osservati (xi)e una costante (c) al quadrato è necessariamente maggiore (o al massimo uguale)alla sommatoria delle differenze tra i caratteri osservati e la media al quadrato.
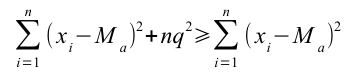
Dimostrazione delle altre proprietà
La [4], la [5] e la [6] non vanno dimostrate.
*Osservazione: la Ma svolgerà effettivamente un ruolo di sintesi soltanto se le diverse modalità assunte dalle unità statistiche saranno abbastanza vicine alla media.
La Ma infatti risente molto dei cosiddetti valori anomali.
Video sulla media aritmetica
Qui sotto puoi vedere un breve video che spiega la media, preso dal nostro canale YouTube:
Esercizi svolti sulla media aritmetica
Vuoi metterti alla prova con degli esercizi svolti? Puoi guardare i video qui sotto!
Esercizi svolti semplici
Esercizi svolti difficoltà media
Domande e risposte
La media aritmetica è un numero che ci riassume qual è il “centro” di una distribuzione.
Più formalmente,è un valore di sintesi dell’osservazione delle modalità assunte da un carattere.
Formalmente la media aritmentica si rappresenta come nell’immagine allegata.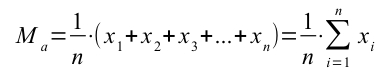
No. La Ma può essere calcolata soltanto per caratteri quantitativi.
Non può essere usata per caratteri qualitativi.
Molto semplicemente, si sommano tutti i valori osservati, e si dividono per il numero di osservazioni.
La media ponderata è uguale alla Ma, con la differenza che ciascuna osservazione ha un “peso”.
Quindi si deve moltiplicare ciascun elemento per il rispettivo peso, e poi dividere tutta la somma per i diversi pesi.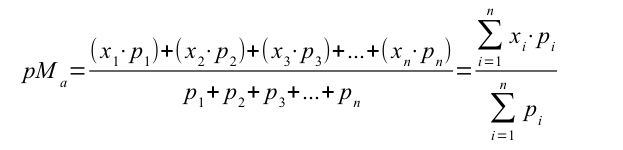
Ci serve semplicemente a rappresentare sinteticamente un collettivo. In particolare, con la media aritmetica vogliamo vedere qual è il “centro” di una certa distribuzione.
La Ma non è l’unico valore di sintesi in grado di rappresentare il centro di una distribuzione, ma ce ne sono anche altri (come la moda o la mediana).
Puoi trovare tanti altri articoli sulla statistica nella pagina dedicata!
Facci sapere cosa ne pensi di questo post lasciando una valutazione qui sotto!
