Sei uno studente di economia e vuoi padroneggiare la teoria del consumatore? Allora devi assolutamente conoscere la curva di indifferenza!
In questo post ti spiegheremo in modo chiaro:
– Cos’è una curva di indifferenza e perché è fondamentale nell’analisi delle scelte del consumatore.
– Quali sono le sue caratteristiche e come interpretarne la forma.
– Come si calcola la sua pendenza, ovvero il saggio marginale di sostituzione.
– Casi particolari, come le curve di indifferenza per beni perfettamente complementari o perfettamente sostituibili.
Se vuoi partire dalle basi, dai un’occhiata al nostro post sulla teoria del consumatore cliccando sul pulsante qui sotto:
In fondo alla pagina toverai anche un video sulla curva di indifferenza, e un quiz per mettere alla prova la tua conoscenza!
Pronto a scoprire tutto sulle curve di indifferenza? Iniziamo!
Rappresentare le preferenze del consumatore sugli assi cartesiani
Il consumatore trae una certa utilità dal consumo di beni e servizi.
Gli economisti sostengono che sia possibile misurare questa utilità. Ad esempio, un consumatore ottiene un’utilità 5 dal consumare un chilogrammo di pane.
Ipotizziamo per semplicità che il consumatore scelga soltanto tra due tipi di beni, ciascuno dei quali gli da una certa utilità: il pane e la pasta.
Una combinazione dei due beni, è detta “paniere” di beni.
Se disegnamo degli assi cartesiani, in cui mettiamo un bene nell’asse delle ascisse (orizzontale)e l’altro bene nell’asse delle ordinate (verticale), ciascun punto rappresenta un paniere di beni (cioé una combinazione dei due beni).
La mappa delle preferenze
Scorri le slide qui sotto per capire meglio come si rappresenta la mappa delle preferenze del consumatore:
In questo grafico, abbiamo il pane (asse orizzontale)e la pasta (asse verticale).
Il punto in rosso rappresenta un paniere composto da 3 kg di pane e 10 kg di pasta.
Il punto in blu rappresenta un paniere con 20 kg di pasta e 6 kg di pane.
Come abbiamo detto, per gli economisti è possibile misurare l’utilità.
Rappresentiamo allora un paniere di pane e pasta che da al consumatore un utilità di 80.
Questo paniere, rappresentato in blu, è dato da 20 kg di pasta, e 2 kg di pane.
Il consumatore, però, può trarre la stessa utilità consumando meno pasta e più pane.
Consumando 16 kg di pasta, e 3 kg di pane (il paniere evidenziato in rosso), il consumatore ha comunque un’utilità di 80 (come per il paniere precedente).
Ci saranno anche altri panieri che danno al consumatore la stessa utilità di 80 (con quantità diverse dei due beni).
Le curve di indifferenza
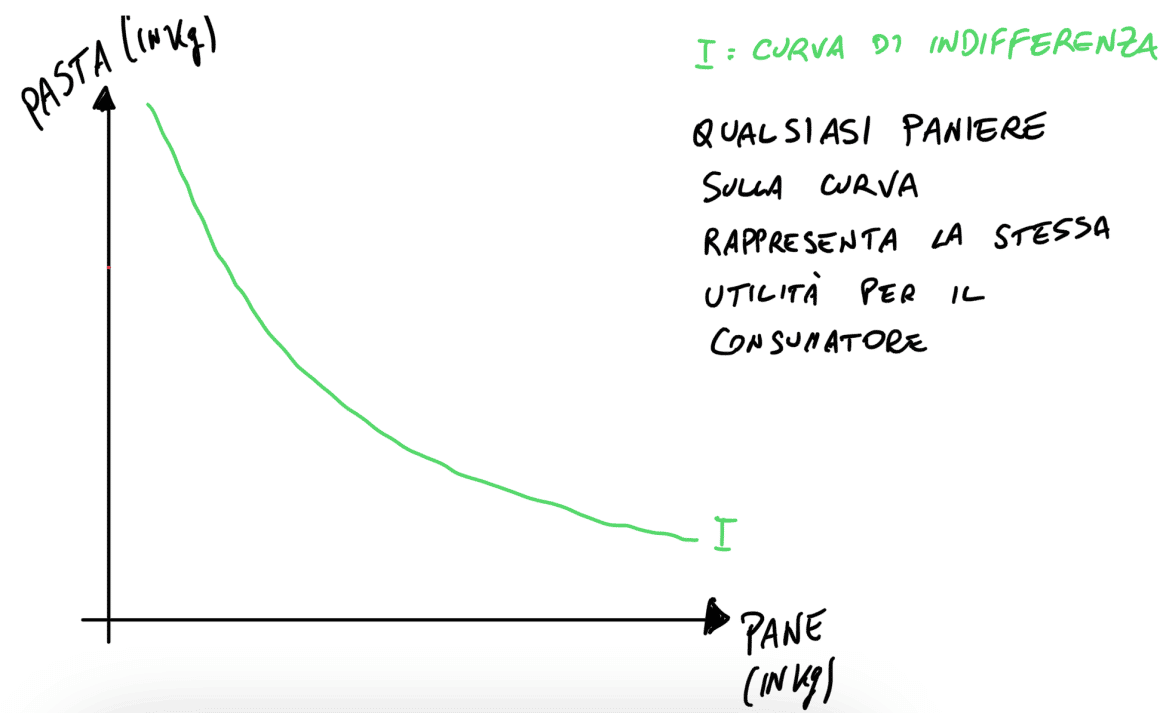
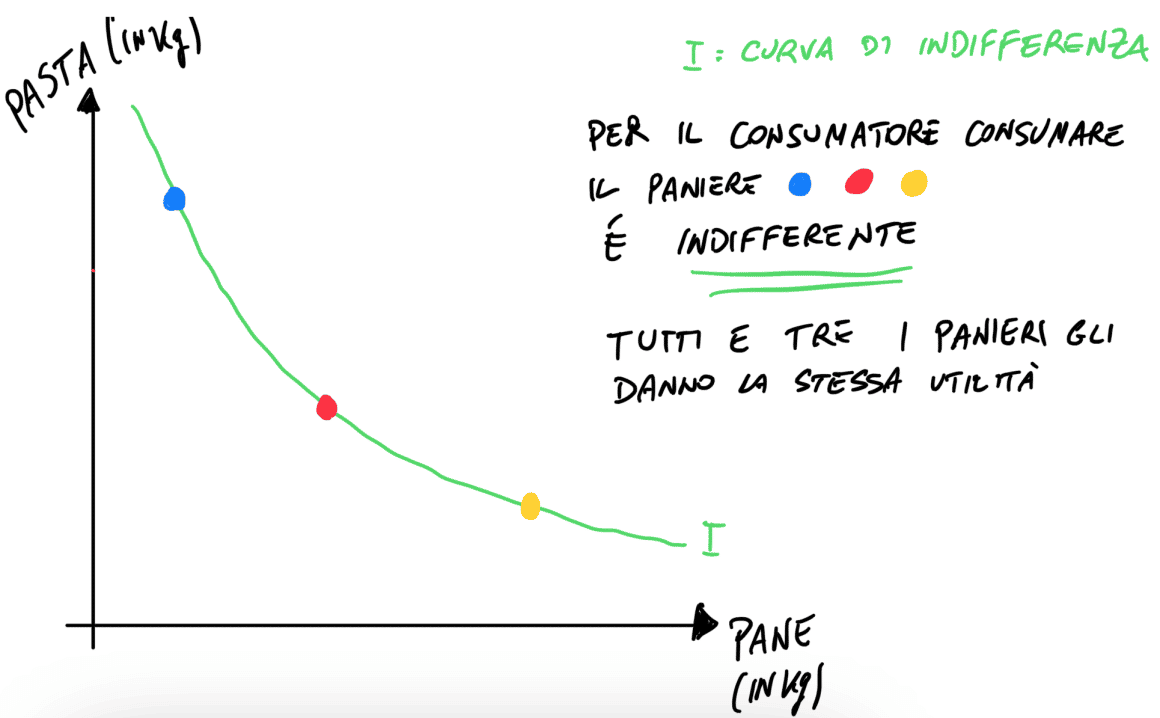
Una curva di indifferenza è semplicemente una funzione che esprime utilità costante lungo se stessa.
Abbiamo visto finora come si possono rappresentare i panieri di beni negli assi cartesiani, e come ciascun paniere da una certa utilità al consumatore.
Vediamo adesso come si passa dalle mappe delle preferenze alla curva di indifferenza.
Vediamo adesso come si passa dalle mappe delle preferenze alla curva di indifferenza.
Dalla mappa delle preferenze alla curva di indifferenza
Scorri le slide qui sotto per vedere come si passa dalle mappe delle preferenze alla curva di indifferenza:
Abbiamo visto precedentemente un esempio in cui un consumatore ottiene un’utilità di 80 consumando 16 kg di pasta, e 3 kg di pane (il paniere evidenziato in rosso), e la stessa utilità (80) consumando invece 20 kg di pasta e 2 kg di pane.
Se mettiamo insieme tutti i panieri che danno al consumatore la stessa utilità (nel nostro esempio un’utilità di 80), otteniamo una curva di indifferenza.
Come vediamo, la curva di indifferenza tracciata in verde passa per i due panieri che danno al consumatore un’utilità pari a 80.
Anche tutti gli altri punti sulla curva di indifferenza danno al consumatore la stessa utilità (nel nostro esempio un’utilità di 80).
Per questo motivo, queste curve sono dette “di indifferenza”.
Per il consumatore è indifferente consumare un paniere piuttosto che un altro, lungo la curva di indifferenza.
Questo perché per i suoi gusti, qualsiasi paniere lungo la curva gli da la stessa utilità.
Caratteristiche della curva di indifferenza
La curva di indifferenza ha tre caratteristiche principali:
1) Ha pendenza negativa
2) L’andamento è variabile*
3) Il grafico è convesso rispetto all’origine*
Le curve di indifferenza non possono mai intersecarsi.
Nei punti 2 e 3 c’è un asterisco perché, come vedremo a breve, ci sono alcuni casi particolari in cui non è così.
Le curve di indifferenza più lontane dall’origine rappresentano un’utilità maggiore
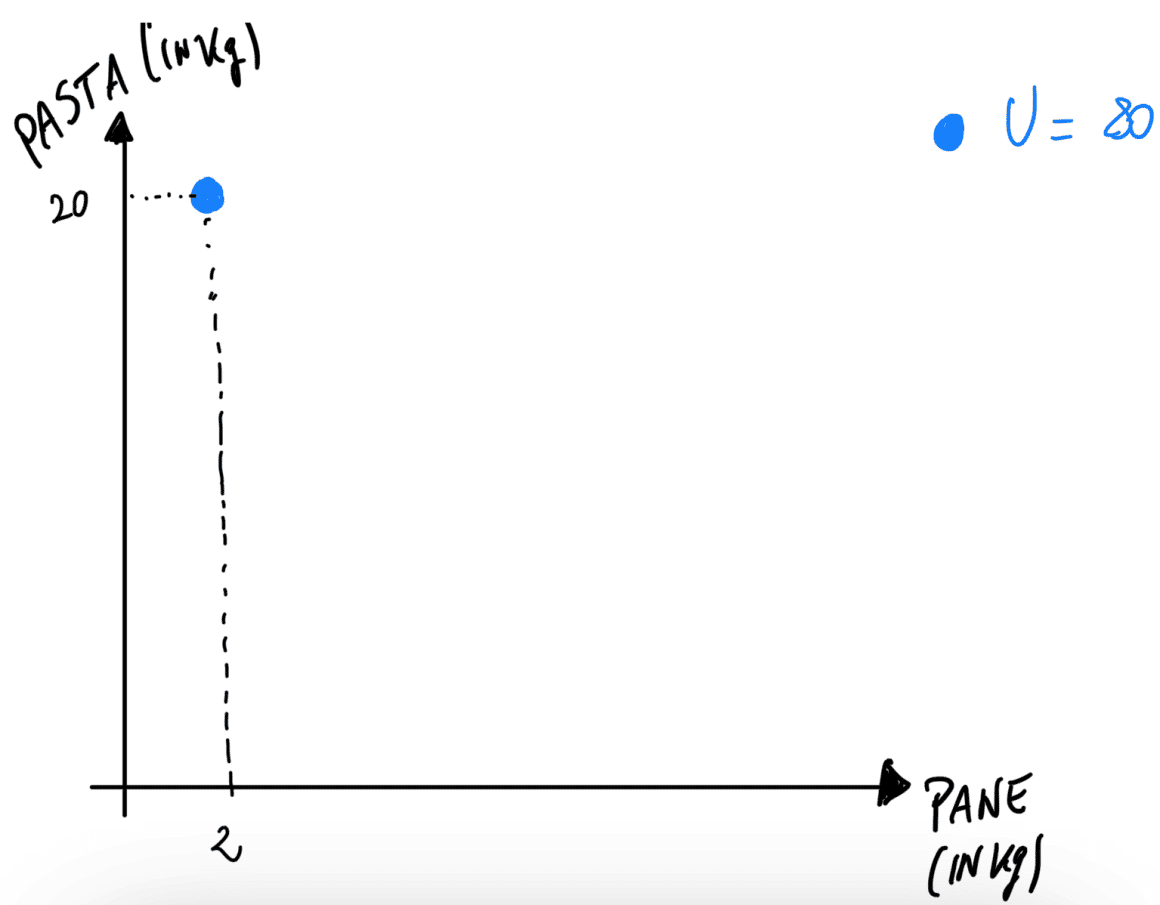
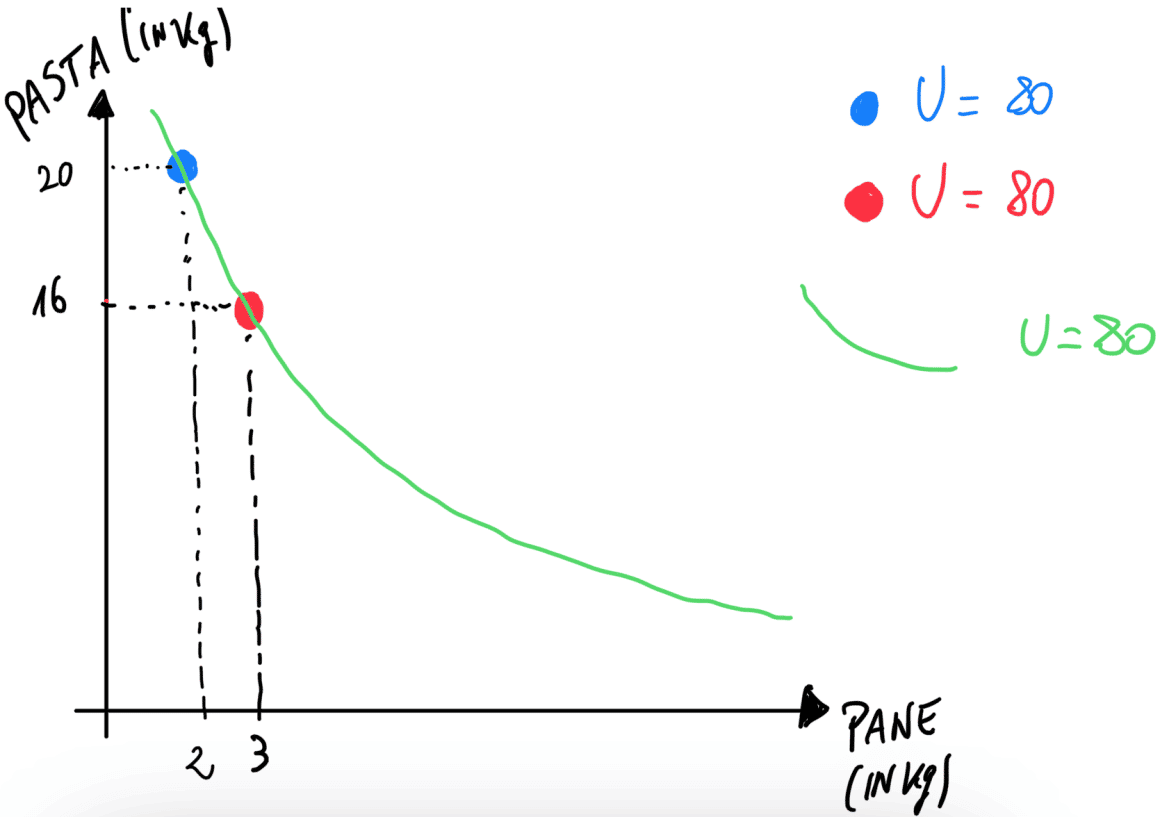
Nel nostro esempio precedente, abbiamo visto una curva di indifferenza che garantisce al consumatore un’utilità pari a 80, con diverse combinazioni di beni lungo di essa.
Ma attenzione: ogni consumatore non ha una sola curva di indifferenza!
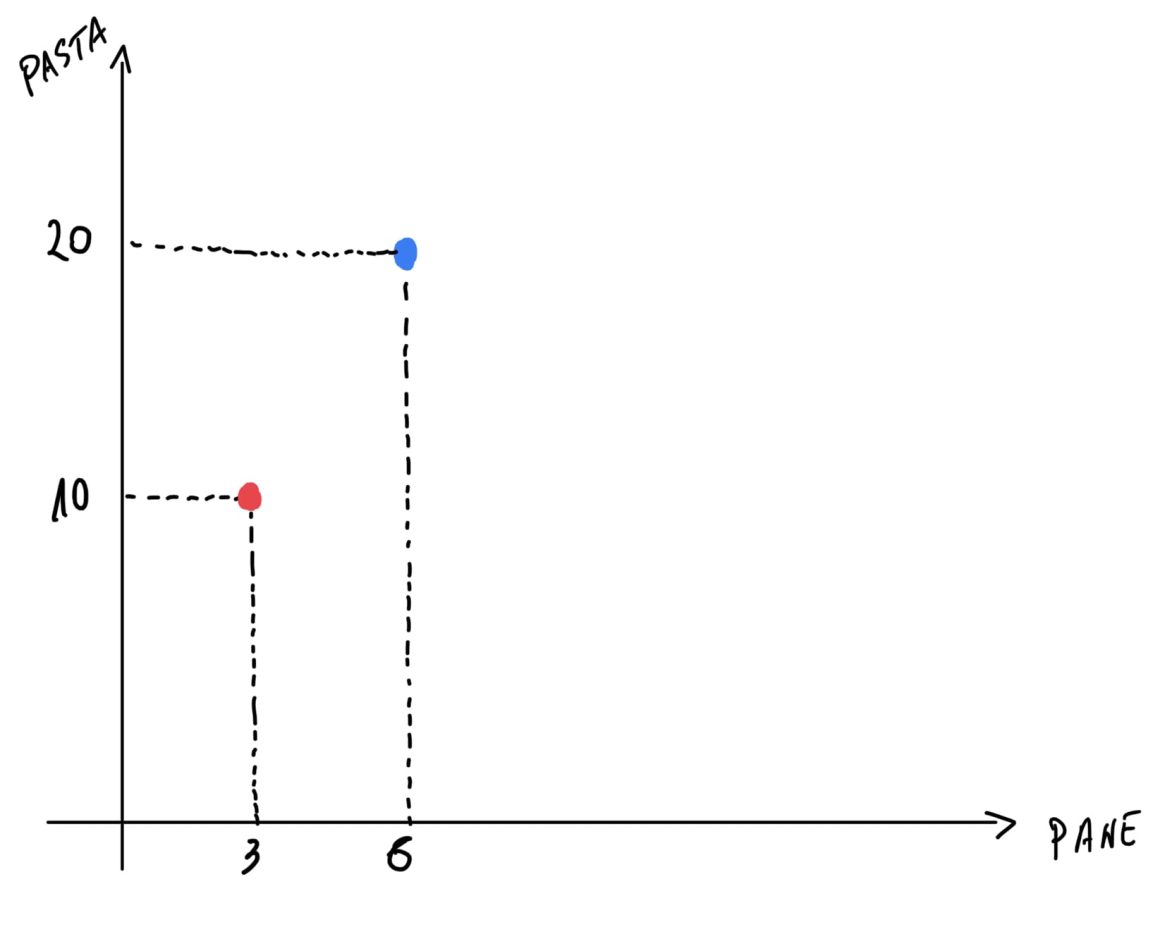
Immaginiamo di spendere tutto il nostro reddito in biglietti del cinema e del teatro. Se ci troviamo su una specifica curva di indifferenza, possiamo scegliere tra diverse combinazioni, come:
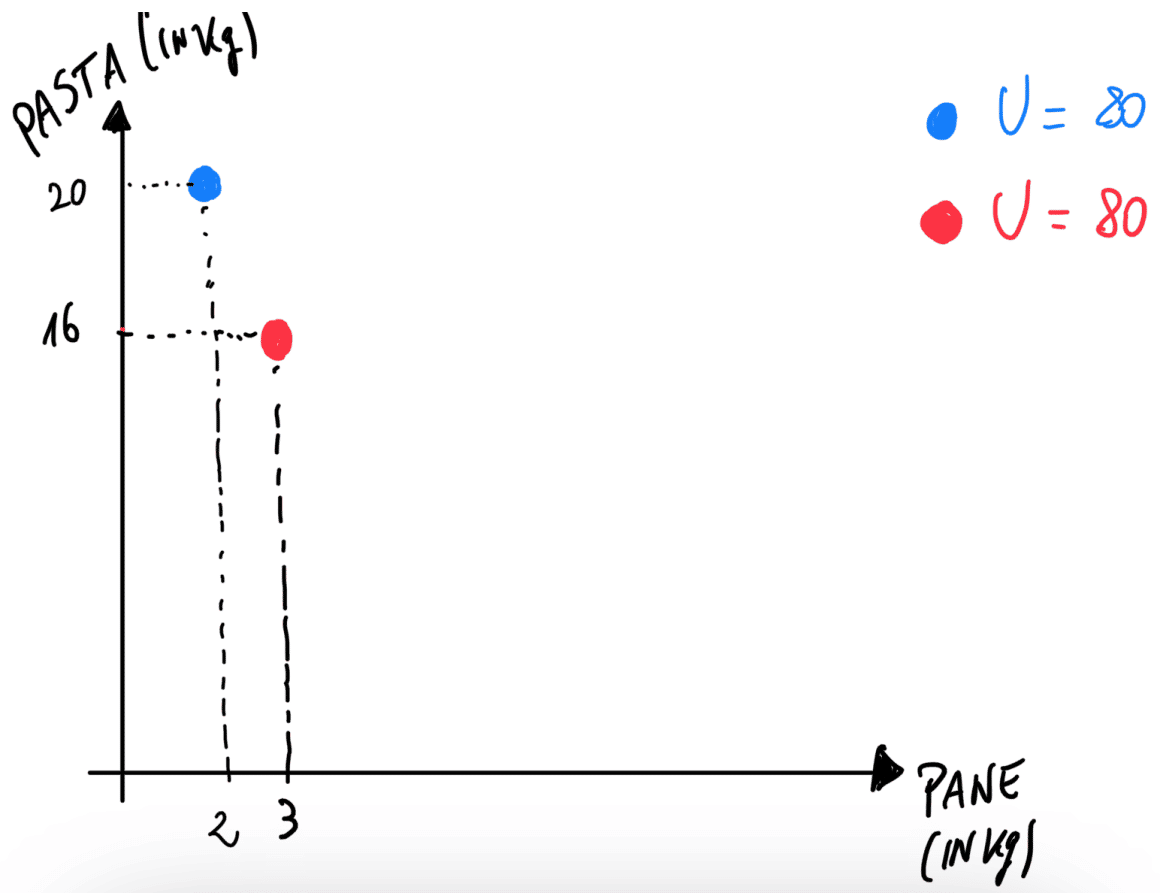
- 20 biglietti del cinema e 2 del teatro
- 16 biglietti del cinema e 3 del teatro
Entrambe le opzioni ci danno lo stesso livello di soddisfazione (utilità).
Ora, ipotizziamo invece di acquistare 100 biglietti del cinema e 10 del teatro. Questa combinazione ci garantisce la stessa utilità delle precedenti? Ovviamente no! Questo nuovo paniere si trova su una curva di indifferenza diversa, più lontana dall’origine degli assi.
E qui arriva il punto chiave: più una curva di indifferenza è distante dall’origine, maggiore è l’utilità che rappresenta. Questo principio si basa sulla non sazietà (un principio delle preferenze del consumatore), ovvero il fatto che, a parità di condizioni, avere più beni è sempre preferibile.
Se guardiamo il grafico, possiamo notare che tra le curve rappresentate, la curva I3 (quella rossa, più lontana dall’origine) è quella che assicura al consumatore il massimo livello di utilità.
In teoria, il consumatore vorrebbe posizionarsi su una curva ancora più lontana, all’infinito. Tuttavia, come sappiamo dalla teoria del consumatore, ciò non è possibile a causa del vincolo di bilancio, che limita le sue scelte in base alle risorse disponibili.
E qui arriva il punto chiave: più una curva di indifferenza è distante dall’origine, maggiore è l’utilità che rappresenta. Questo principio si basa sulla non sazietà (un principio delle preferenze del consumatore), ovvero il fatto che, a parità di condizioni, avere più beni è sempre preferibile.
Se guardiamo il grafico, possiamo notare che tra le curve rappresentate, la curva I3 (quella rossa, più lontana dall’origine) è quella che assicura al consumatore il massimo livello di utilità.
In teoria, il consumatore vorrebbe posizionarsi su una curva ancora più lontana, all’infinito. Tuttavia, come sappiamo dalla teoria del consumatore, ciò non è possibile a causa del vincolo di bilancio, che limita le sue scelte in base alle risorse disponibili.
La pendenza della curva di indifferenza – Il saggio marginale di sostituzione (MRS o SMS)
La pendenza delle curve di indifferenza ci dice quante unità di un bene siamo disposti a sacrificare per ottenere un’unità aggiuntiva dell’altro bene, mantenendo invariata la nostra utilità.
Questa pendenza è sempre negativa. Perché? Perché, se vogliamo più di un bene, dobbiamo rinunciare a una certa quantità dell’altro. Questo principio riflette il trade-off nelle scelte del consumatore: non possiamo avere tutto illimitatamente, quindi dobbiamo fare delle sostituzioni.
La pendenza della curva di indifferenza prende il nome di MRS (Marginal Rate of Substitution), ovvero Saggio Marginale di Sostituzione (SMS) in italiano. Questi due termini sono equivalenti, quindi in questo post useremo MRS per semplicità.
Ma come si calcola l’MRS?
Si ottiene dividendo la variazione della quantità consumata di un bene per la variazione della quantità consumata dell’altro bene.
Ipotizziamo di avere il bene 1 (la cui quantità consumata è q1) e il bene 2, la cui quantità consumata è q2.
In questo caso, il saggio marginale di sostituzione si calcola così:
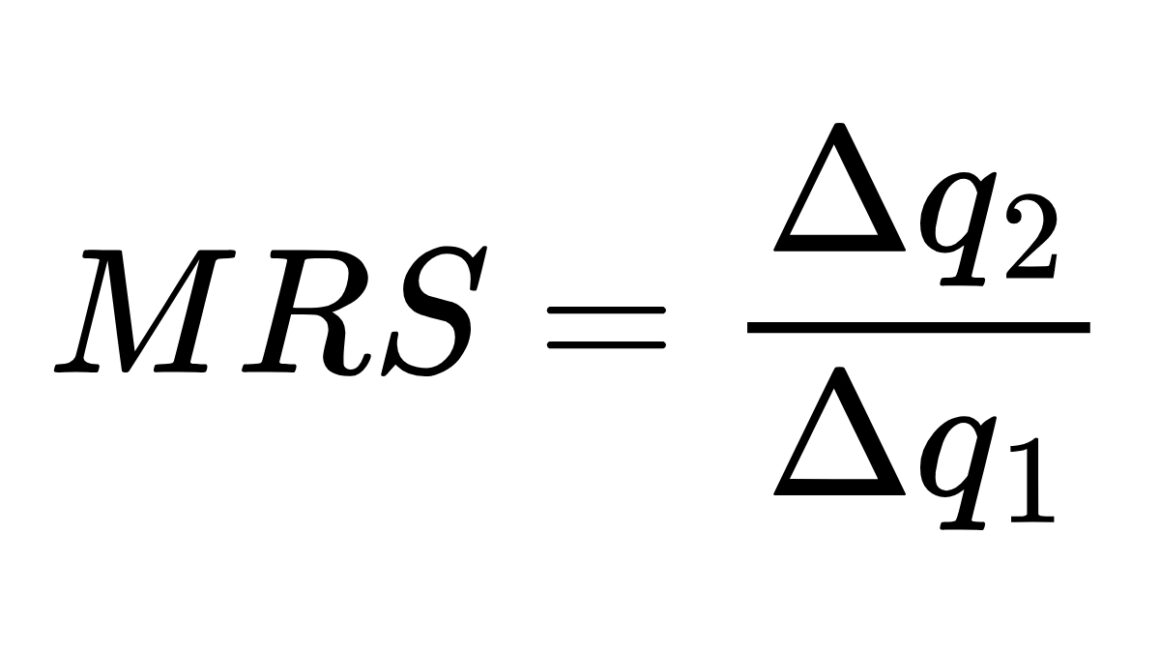
Dove:
- q1 e q2 rappresentano le quantità consumate dei due beni (q2 è il bene sulle ordinate e q1 è il bene sulle ascisse.
- Δq2 rappresenta la variazione della quantità del bene 2.
- Δq1 rappresenta la variazione della quantità del bene 1.
- Il segno negativo indica che, per ottenere più di un bene, dobbiamo rinunciare a una parte dell’altro
Il saggio marginale di sostituzione (MRS o SMS) è un concetto fondamentale nella teoria del consumatore, perché ci aiuta a capire le preferenze individuali e il modo in cui un consumatore è disposto a sostituire un bene con un altro. Ad esempio, quanti popcorn saresti disposto a scambiare per un biglietto del cinema in più? Dipende dal valore soggettivo che attribuisci ai due beni!
Legge del saggio marginale di sostituzione decrescente
Osserviamo che il saggio marginale di sostituzione è via via inferiore. Per spiegarlo meglio scorriamo le slide qui sotto:
Nel punto A il soggetto consuma:
- 24 unità del bene Y (asse verticale – Ordinate)
- 1 sola unità del bene X (asse orizzontale – Ascisse).
A quante unità di Y deve rinunciare per consumare un’unità in più del bene X?
Vediamolo nell’immagine successiva.
Vediamo che per consumare un’unità in più del bene X (e quindi 2 unità in totale), il consumatore deve rinunciare a 5 unità del bene Y.
Cosa succede se vuole consumare un’ulteriore unità in più del bene X (e quindi consumarne 3 in totale)?
A quante unità del bene Y deve rinunciare?
Vediamolo nella slide successiva.
Per consumare un’altra unità del bene X, e quindi andare nel punto C, deve rinunciare a 3 unità del bene Y (mentre prima ha dobuto rinunciare a 5).
Andiamo ancora avanti. Cosa succede se il consumatore vuole un’altra unità del bene X?
Per consumare una quarta unità del bene X, e andare nel punto D, deve rinunciare comunque a 3 unità del bene Y, come prima.
Potremmo continuare così per ciascuna unità.
Ma facciamo finta che il consumatore adesso consumi soltanto 3 unità del bene Y.
Vediamolo nella slide successiva.
Nel punto E, il soggetto consuma:
- 3 unità del bene Y
- 16 unità del bene X
A questo punto, per la legge del saggio marginale decrescente, ci aspettiamo che per ottenere un’unità in più di X debba rinunciare a poco della quantità del bene Y.
Confermiamolo nella slide successiva.
Per consumare un’unità aggiuntiva del bene X (e quindi spostarsi dal paniere E al paniere F sulla curva di indifferenza), il consumatore deve rinunciare a una frazione del bene Y (0,3).
Questo significa che mentre per spostarsi da A a B rinunciava a 5 unità del bene Y, per spostarsi da E a F, rinuncia soltanto a 0,3 unità.
In entrambi i casi, consuma una sola unità in più del bene X.
Vediamo lo stesso concetto in un’altra immagine, che mette in evidenza ancora meglio come funziona la legge del saggio marginale di sostituzione decrescente.
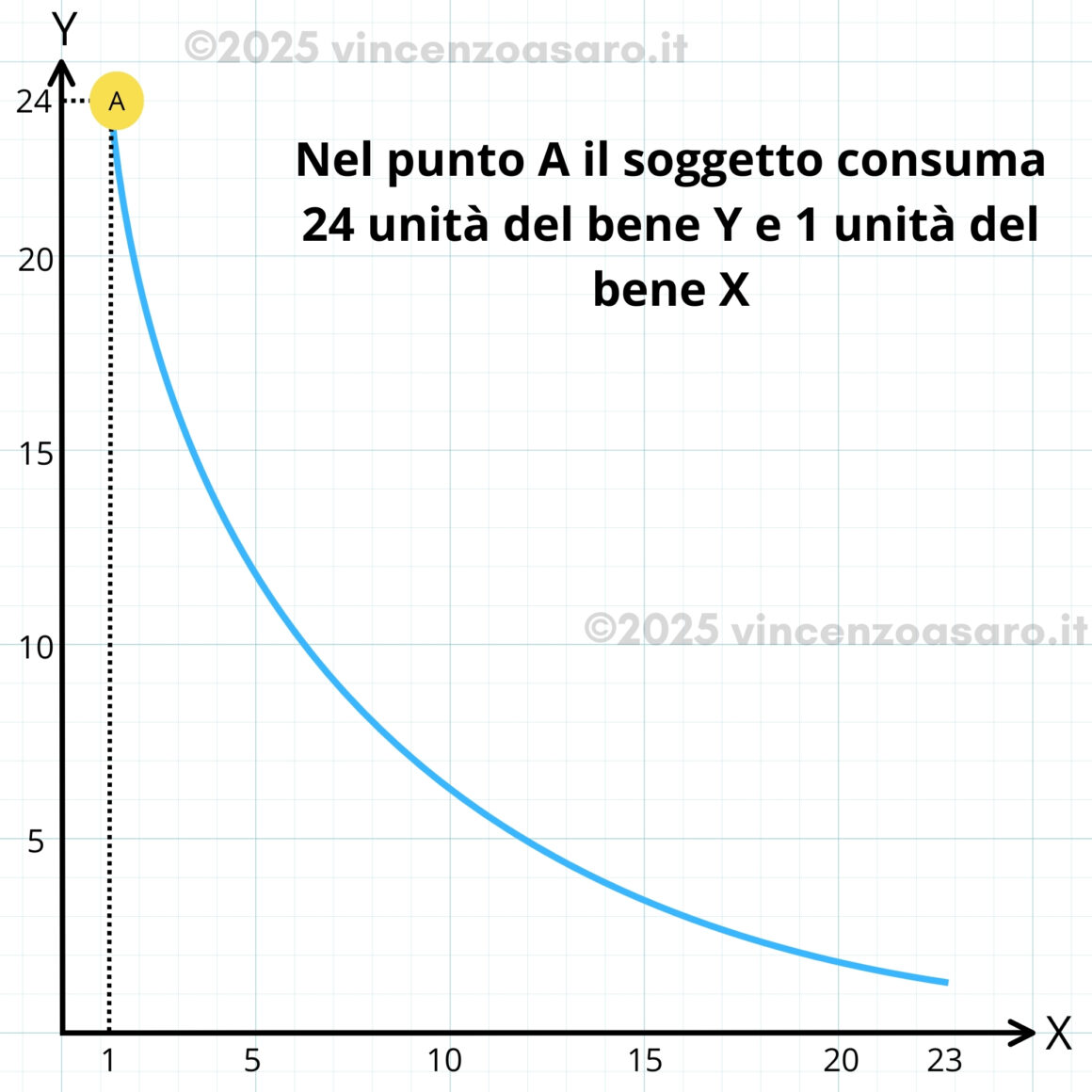
Come si può vedere nel grafico:
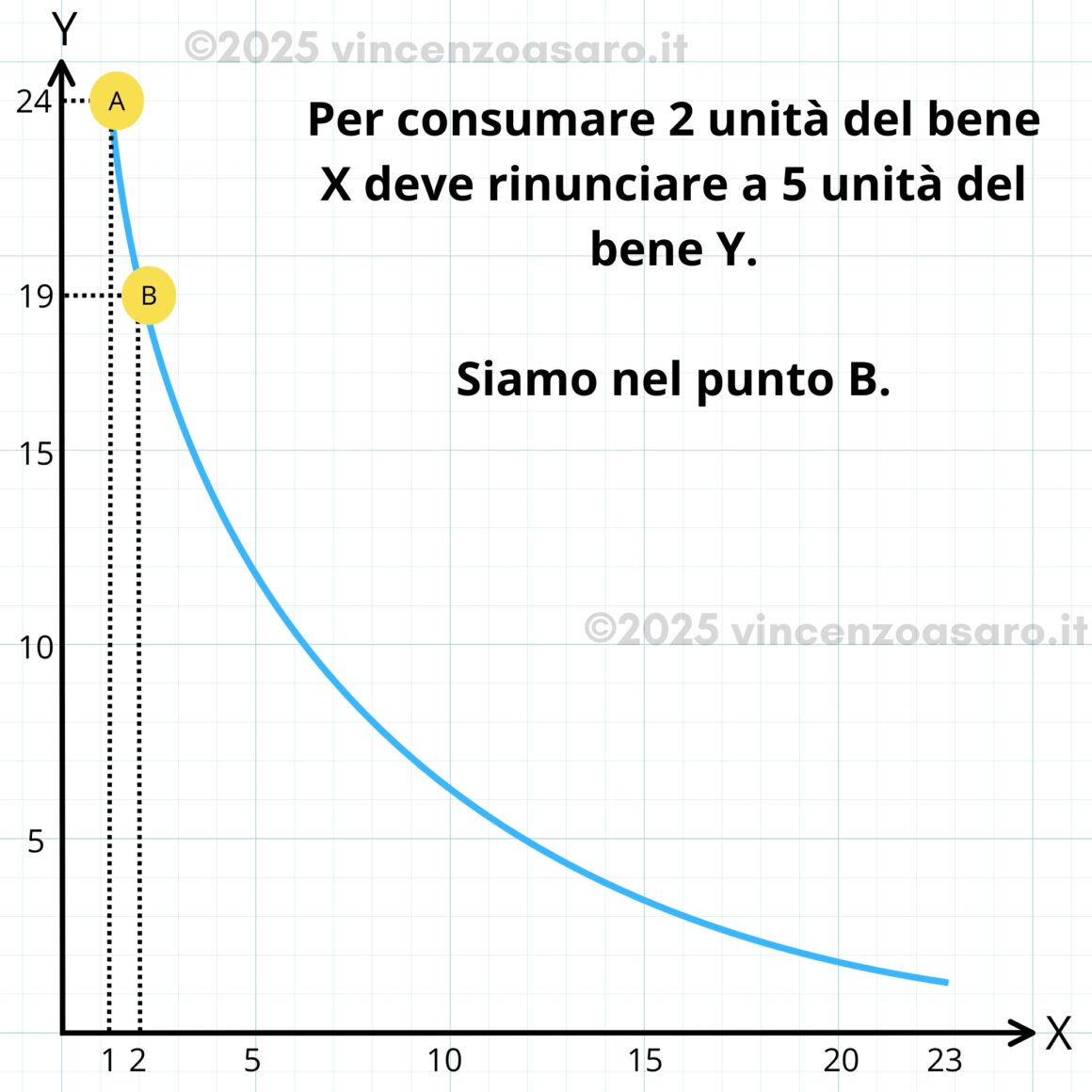
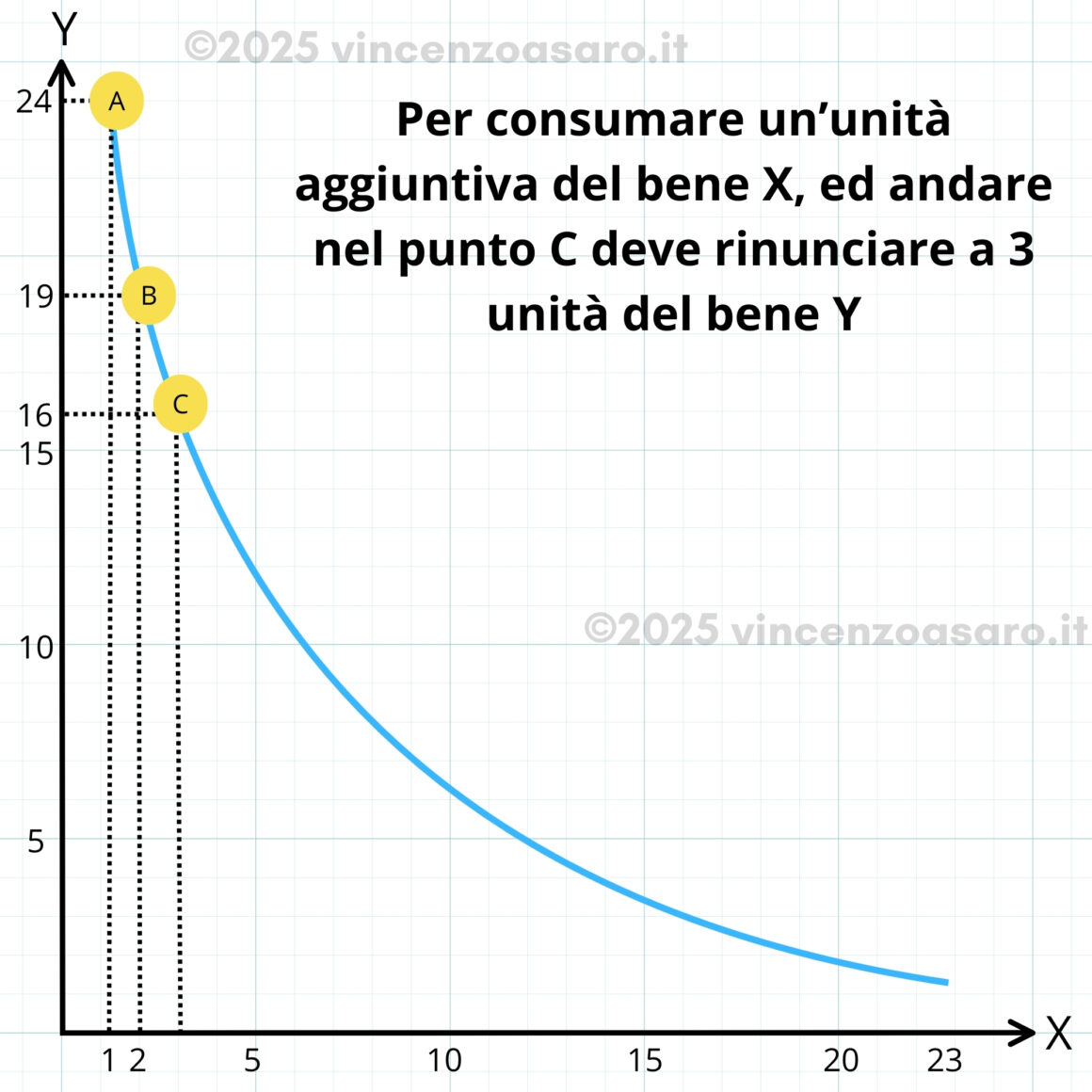
- per passare da A a B, il consumatore rinuncia a 6 unità di un bene per ottenerne una dell’altro bene.
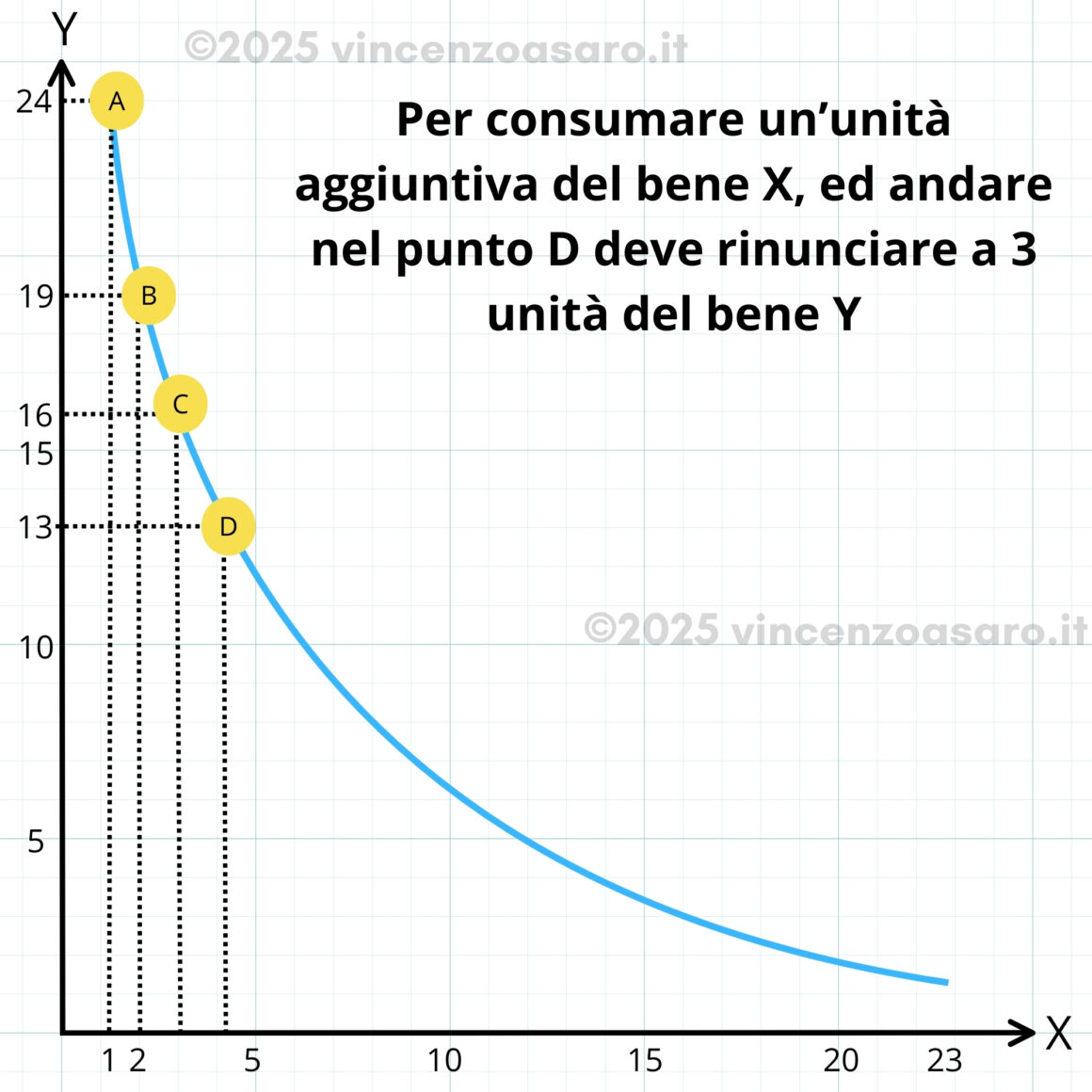
MRS = -6 - Poi, per passare da B a D, rinuncia a 4 unità per l’unità aggiuntiva dell’altro bene.
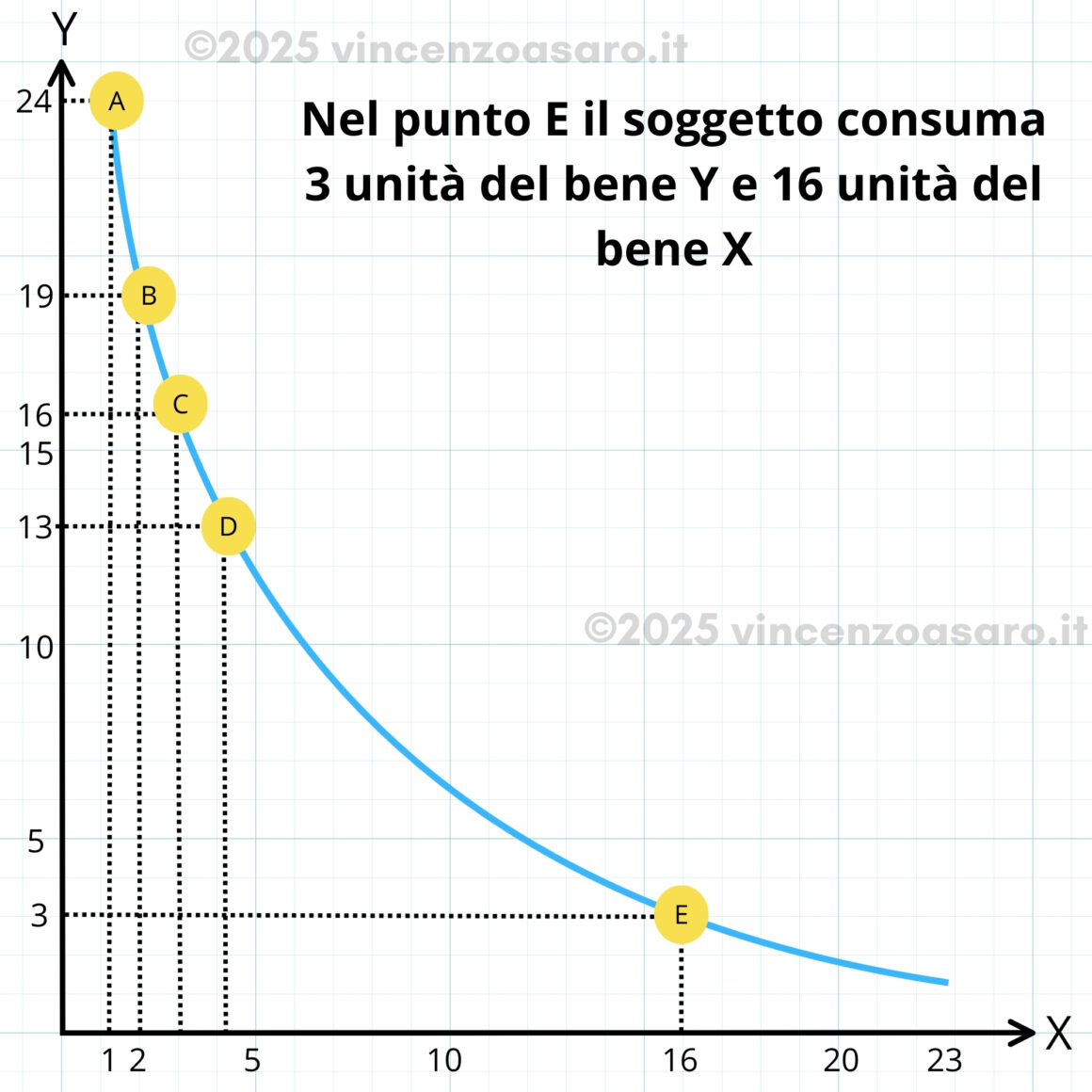
MRS = -4 - Successivamente, per passare da D ad E rinuncia soltanto a due unità.
MRS = -2 - E così via…
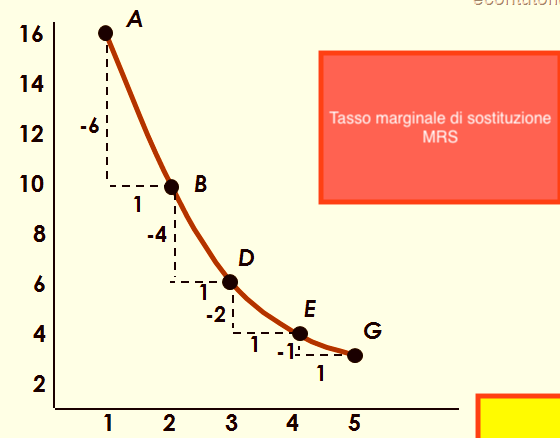
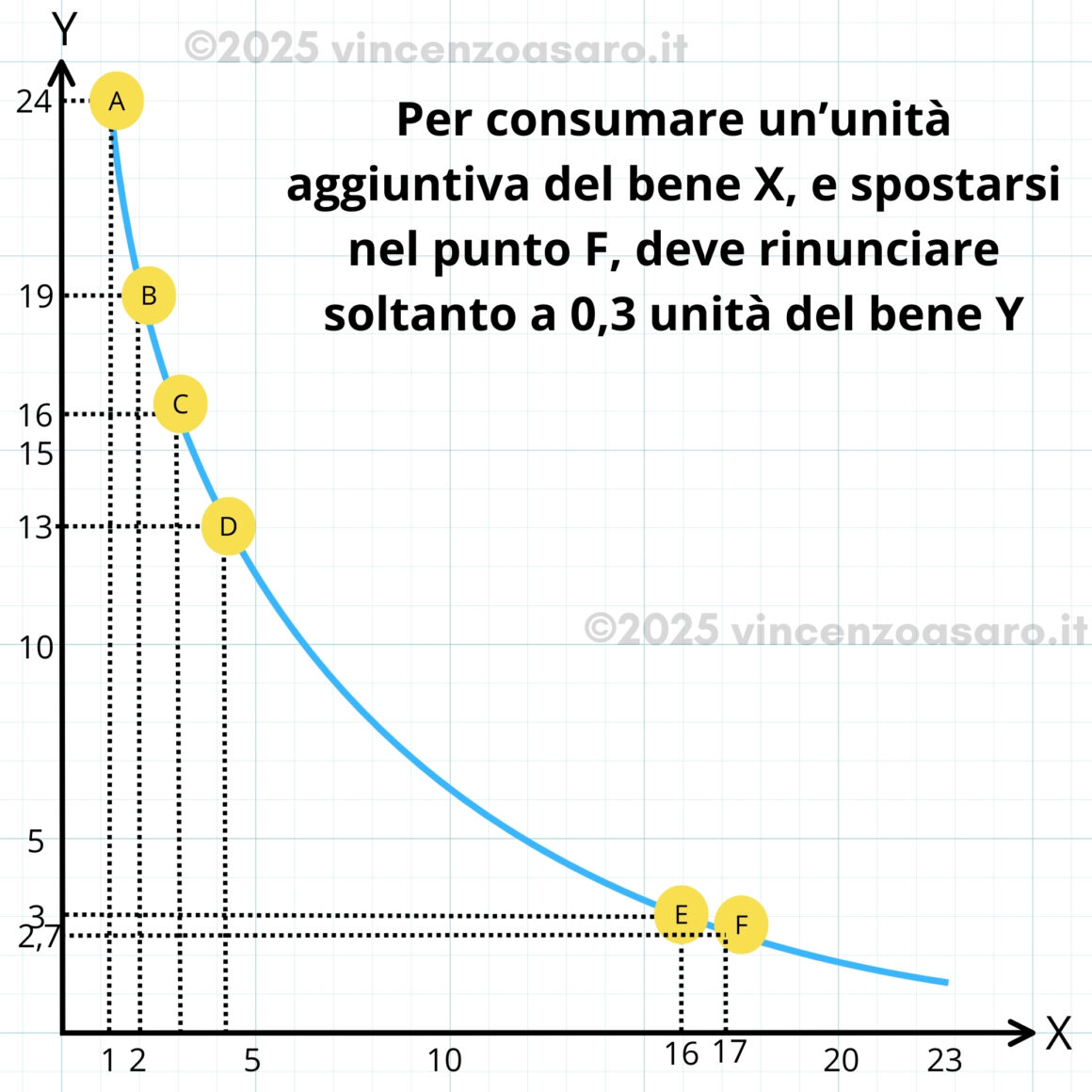
Il concetto da comprendere è che il saggio marginale di sostituzione (MRS)non è lo stesso lungo tutta la curva.
Questo fatto cambia soltanto in alcuni casi particolari, di cui parleremo adesso.
Curva di indifferenza: casi particolari
Quando i due beni messi a confronto sono dei perfetti sostituti, o dei perfetti complementi, allora le cose cambiano.
Il grafico della curva di indifferenza non è più convesso rispetto all’origine, e MRS non è più variabile.
Curve di indifferenza per beni perfetti sostituti
Due beni sono sostituti perfetti quando entrambi i beni hanno per il soggetto la stessa utilità.
In altre parole, per il consumatore acquistare uno o l’altro bene è esattamente la stessa cosa.
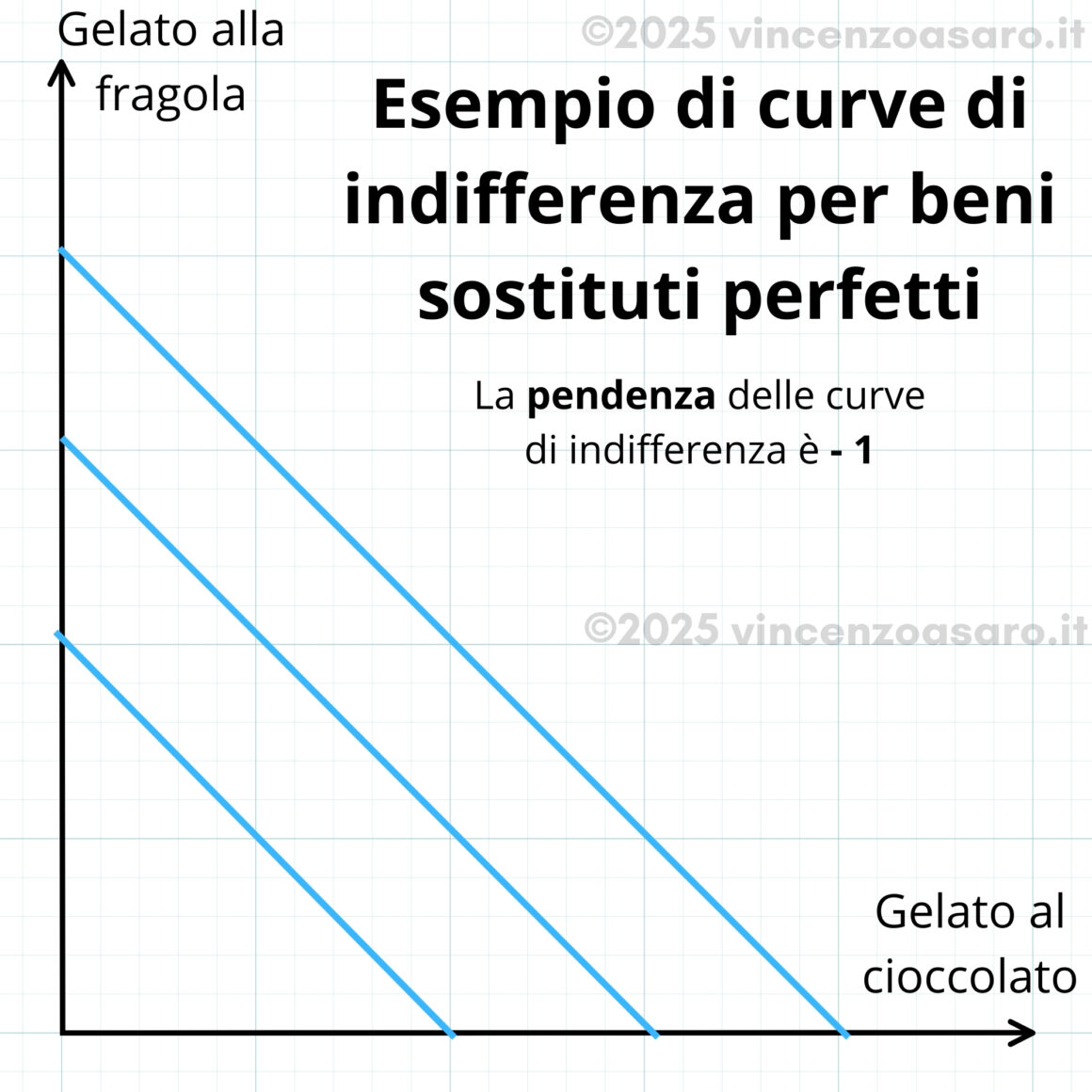
In questi casi, la pendenza è costante (ovvero MRS = k).
Vediamolo nel grafico, in cui sono rappresentate le curve di indifferenza di un soggetto a cui il gelato alla fragola e il gelato al cioccolato piacciono esattamente allo stesso modo.
Curve di indifferenza per beni perfetti complementi
Ad un dato soggetto possono non piacere due beni da soli, ma soltanto se consumati insieme: in questo caso si parla di complementi perfetti.
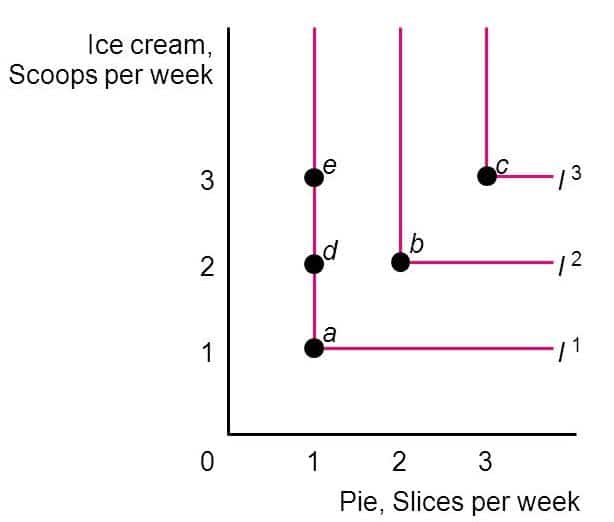
In questo grafico, il consumatore ha utilità soltanto se consuma la torta insieme alle palline di gelato. Quindi si collocherà nei punti a, b oppure c (non in d o e, o in qualsiasi altro punto che non passi lungo la bisettrice).
Video sulla curva di indifferenza
Quiz sulla curva di indifferenza
Se vuoi mettere alla prova la tua conoscenza, puoi completare un breve quiz cliccando sul pulsante qui sotto:
Facci sapere cosa ne pensi di questo post lasciando una valutazione qui sotto!
