Hai mai sentito parlare del Break Even Point (o punto di pareggio)? Se stai studiando economia, gestione aziendale o sogni di avviare un’attività, questo concetto è fondamentale!
Ti sei mai chiesto quante unità devi vendere per coprire tutti i costi e iniziare davvero a guadagnare? Il Break Even Point ti dà la risposta! In questa guida scoprirai:
– Cos’è e perché è così importante
– Come si calcola, passo dopo passo
– Quali sono i suoi vantaggi e i suoi limiti
Preferisci un video che spiega tutto in modo chiaro? Nessun problema! Troverai il link al nostro video sul Break Even Point qui sotto o alla fine della pagina.
Inoltre, in fondo troverai anche domande e risposte frequenti e un’infografica riassuntiva per fissare i concetti chiave. Se vuoi vedere il Break Even Point applicato a un esempio pratico, abbiamo preparato un caso concreto che puoi esplorare con un semplice click!
Pronto? Cominciamo!
- Cos'è il Break Even Point
- Rappresentazione grafica del Break Even Point
- Determinazione analitica del Break Even Point
- Esempi pratici di calcolo del Break Even Point
- Vantaggi e svantaggi del modello del punto di pareggio
- Domande e risposte sul Break Even Point
- Infografica Break Even Point
- Video sul punto di pareggio
Cos’è il Break Even Point
Il Break Even Point (BEP) non è solo un concetto teorico, ma un vero e proprio strumento pratico per prendere decisioni aziendali in modo strategico. Ti sei mai chiesto quante unità di prodotto devi vendere per coprire tutti i costi? Il BEP ti dà la risposta!
Come funziona?
– Se vendi più unità rispetto al punto di pareggio, generi un utile
– Se vendi meno, subisci una perdita
– Se vendi esattamente al BEP, copri tutti i costi senza guadagnare né perdere
In parole semplici, il Break Even Point risponde alla domanda chiave:
“Quante unità devo produrre e vendere affinché costi e ricavi si bilancino?”
Definizione:
Il Break Even Point (o punto di pareggio) è il livello di produzione e vendita in cui i ricavi totali sono esattamente uguali ai costi totali.
Qualche chiarimento utile:
– Break Even Point e punto di pareggio sono la stessa cosa. Se trovi entrambi i termini, non farti confondere!
– In questa guida analizzeremo il BEP per aziende monoprodotto. Se un’azienda produce più prodotti, la situazione diventa più complessa (ma non impossibile da gestire!).
Ora che hai capito il concetto base, vediamo come si calcola e quali sono i suoi limiti!
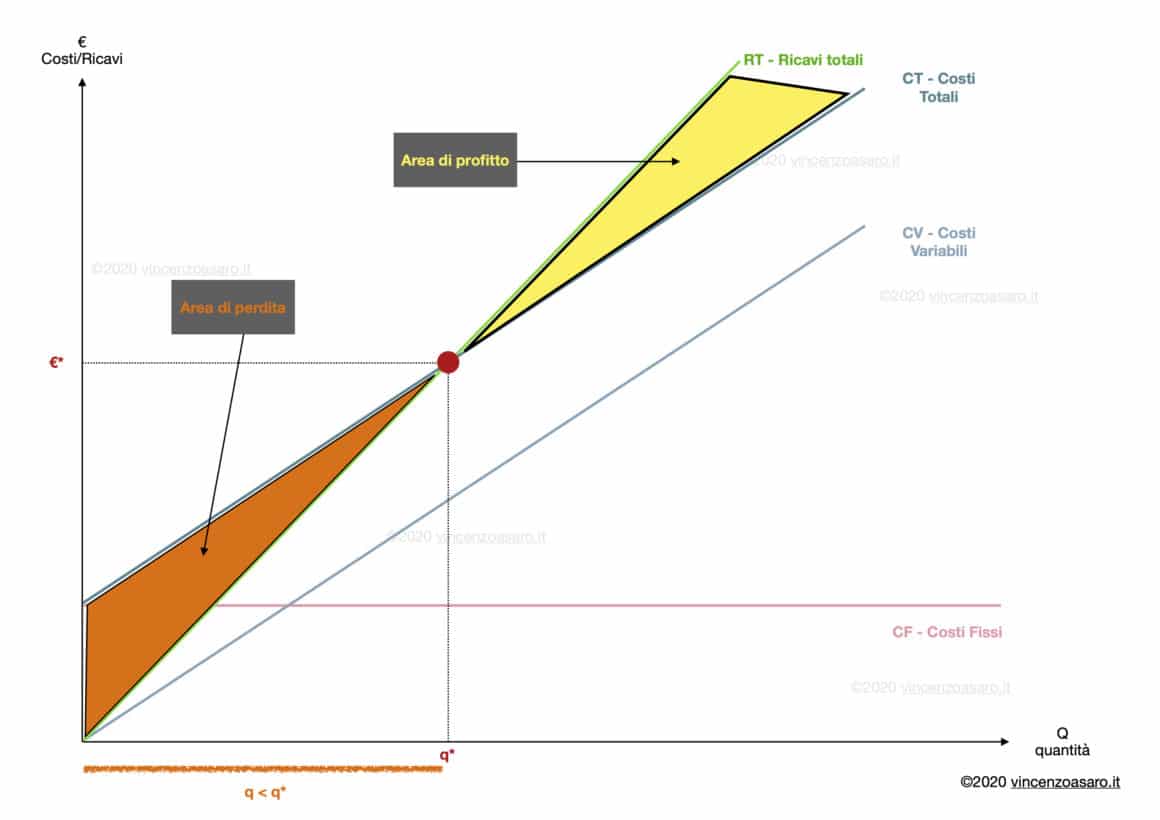
Rappresentazione grafica del Break Even Point
Il punto di pareggio è rappresentato graficamente dal punto di intersezione tra ricavi totali e costi totali.
Vediamo passo per passo come si compone il grafico del BEP.
1. Disegnare gli assi cartesiani
Gli assi cartesiani, nella rappresentazione del BEP, sono la quantità (asse delle ascisse)e i costi/ricavi (asse delle ordinate).

2. I costi nel grafico del punto di pareggio
Nel calcolo del Break Even Point teniamo conto dei costi fissi, di quelli variabili e di quelli totali (che sono la somma dei costi fissi e dei costi variabili).
Vediamoli singolarmente.
a. I costi fissi
I costi fissi, sono quei costi che non variano al variare della quantità prodotta.
Esempi di costi fissi possono essere:
- l’affitto dei fabbricati nei quali si trova l’azienda (l’affitto si paga a prescindere da quanto si produce. Anche con produzione zero, l’affitto rimane lo stesso).
- Gli stipendi dei dipendenti (una volta che si è assunto un dipendente, il suo stipendio è fisso, a prescindere dalla quantità prodotta e venduta dall’impresa).
Dunque i costi fissi sono una costante, e in quanto tali vengono rappresentati attraverso una retta orizzontale.

b. I costi variabili
I costi variabili, sono quei costi che variano al variare della quantità prodotta.
Esempi di costi variabili possono essere:
- I costi di acquisto delle materie prime
- I costi energetici per far funzionare i macchinari (ad esempio, il consumo energetico di una macchina confezionatrice. Se non si produce niente, la macchina resta spenta, e questo costo viene meno. Altrimenti, quando si accende e si usa, i costi aumentano a seconda del tempo di utilizzo, e quindi della quantità prodotta).
I costi variabili, quindi, sono diversi dai costi fissi. Variano al variare della quantità prodotta.
In particolare aumentano all’aumentare della quantità prodotta.
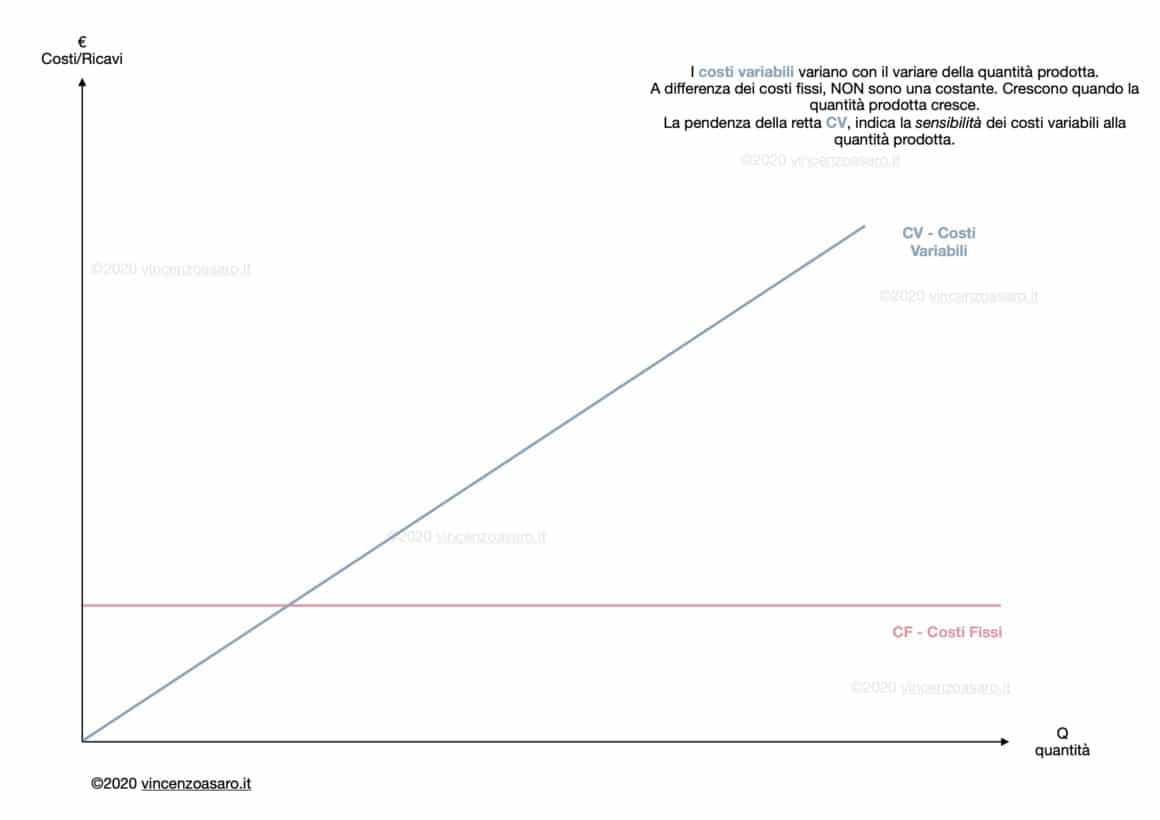
Di conseguenza, la retta dei costi variabili è una retta inclinata verso l’alto (con pendenza positiva).
La pendenza dei costi variabili
La pendenza della retta misura di quanto aumentano i costi all’aumentare della quantità prodotta.
Se la retta è più inclinata verso l’alto, significa che i costi aumentano rapidamente. Mentre se una retta è più “piatta“, significa che i costi aumentano meno rapidamente.
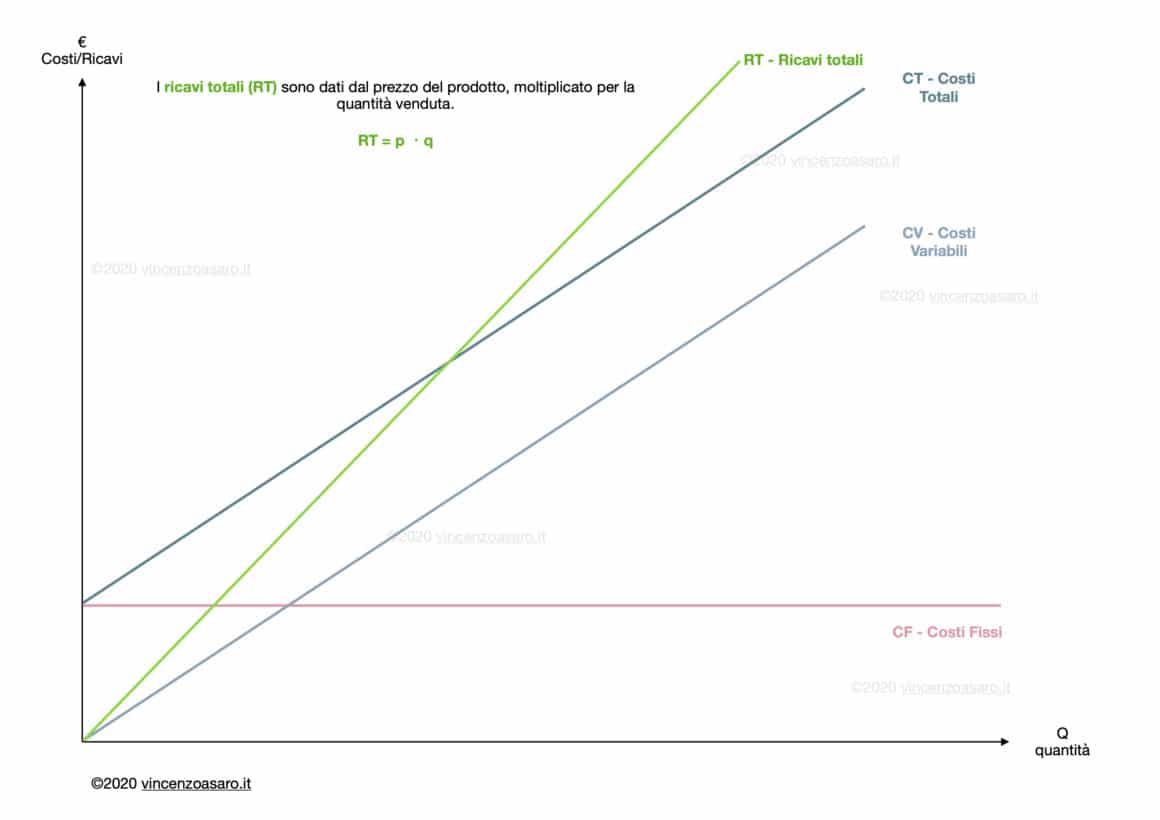
c. I costi totali
I costi totali (che indichiamo con CT) rappresentano la somma di costi fissi e costi variabili.
COSTI TOTALI = COSTI FISSI + COSTI VARIABILI
Quindi, la retta che rappresenta i costi totali sarà identica a quella che rappresenta i costi variabili, MA traslata verso l’alto.
In particolare, la curva dei costi totali è spostata verso l’alto della misura dei costi fissi.

A questo punto, abbiamo finito con la rappresentazione grafica dei costi.
Passiamo alla rappresentazione dei ricavi.
3. I ricavi
I ricavi totali dell’impresa (che rappresentiamo con RT), nel modello, sono rappresentati dalla quantità venduta per il prezzo al quale è stata venduta.
RICAVI TOTALI = PREZZO X QUANTITÀ
Esempio: ipotizziamo di produrre scarpe. Se un paio di scarpe ha un prezzo di 10 €, e ne vendiamo soltanto un paio, il nostro ricavo sarà 10 * 1 = 10 €. Se invece ne vendiamo 5 paia, il nostro ricavo sarà 10 * 5 = 50
Quindi, la pendenza della retta dei ricavi totali (ossia il suo coefficiente angolare)è dato dal prezzo.
Se il prezzo è più alto, la retta sarà più ripida. Se invece il prezzo è più basso, la retta sarà più piatta.
4. Il punto di pareggio (Break Even Point)
Come abbiamo già detto all’inizio, il punto di pareggio (BEP)è il punto di intersezione tra i costi totali e i ricavi totali.
PUNTO DI PAREGGIO:
RICAVI TOTALI = COSTI TOTALI
Graficamente avremo:
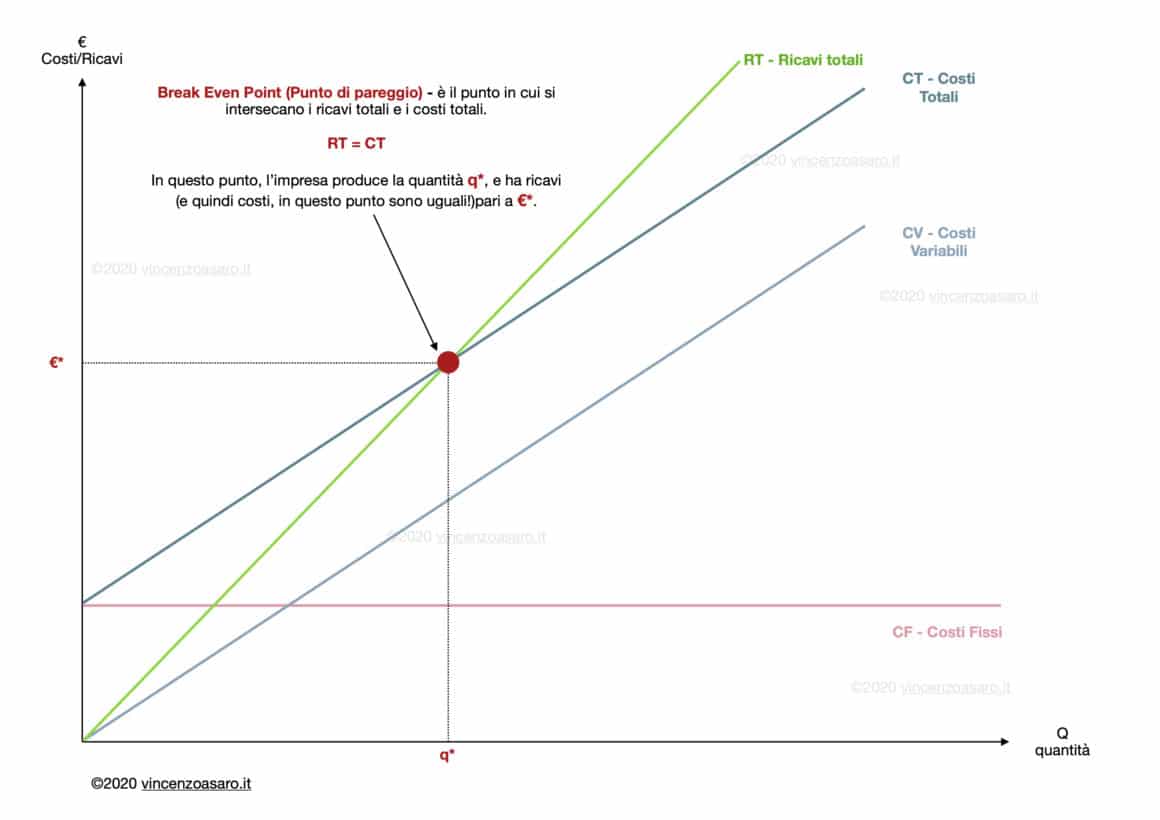
In corrispondenza del punto di pareggio, l’impresa vende la quantità q*, e ha ricavi (uguali ai costi) pari a €*.
Notiamo due cose:
- A destra di q*, quindi per quantità maggiori, la curva dei ricavi totali si trova SOPRA la curva dei costi totali.
Significa che per quantità maggiori, i ricavi totali sono maggiori dei costi totali - A sinistra di q*, quindi per quantità inferiori, la curva dei ricavi totali si trova al di SOTTO della curva dei costi totali.
Significa che per quantità minori di q*, i costi totali superano i ricavi totali (l’impresa è in perdita).
Da quest’ultima osservazione, possiamo introdurre i concetti di area di profitto e area di perdita.
Area di profitto
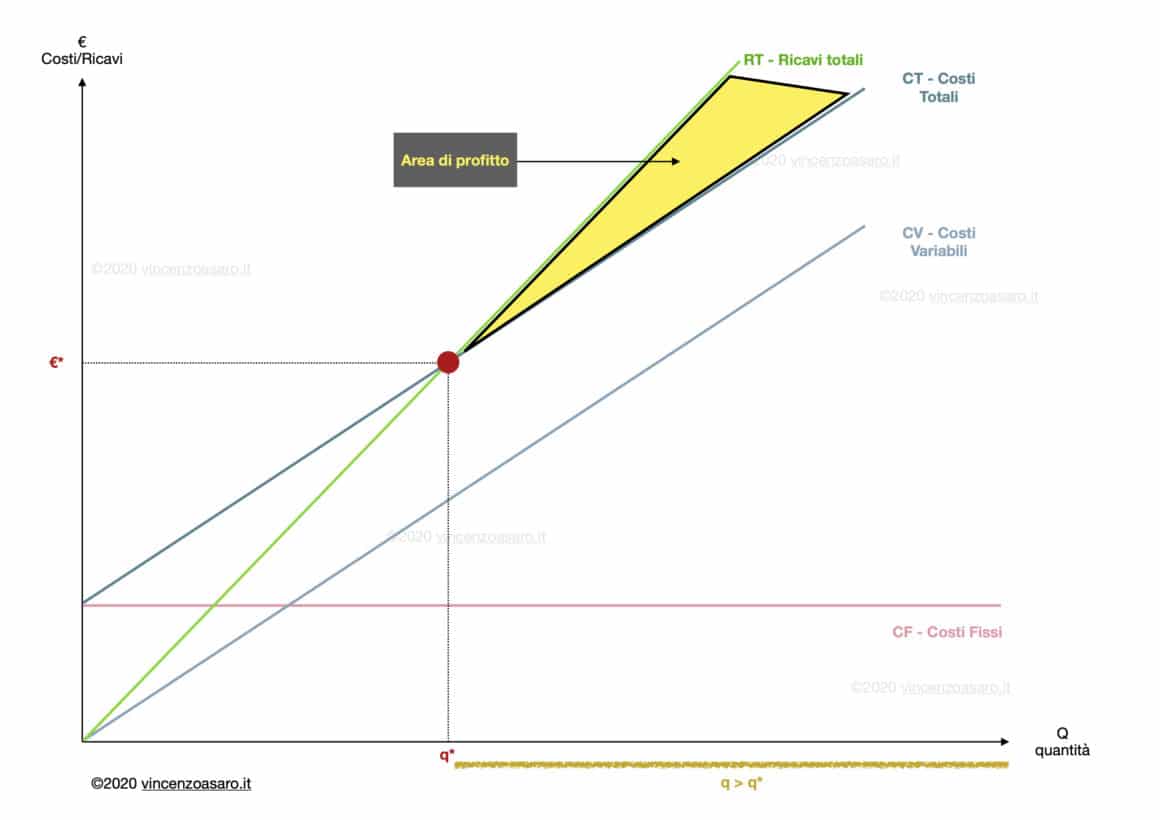
Sappiamo che l’area al di sotto dei ricavi totali è l’area dei ricavi totali.
A questa, dobbiamo però sottrarre l’area sottesa alla retta dei costi totali.
Ciò che ci rimane è l’area evidenziata in giallo, ovvero l’area di profitto.
In quest’area abbiamo profitto perché i ricavi totali sono maggiori dei costi totali.
Area di perdita
Sempre per lo stesso principio, a sinistra del punto di pareggio, abbiamo l’area di perdita (in cui i ricavi totali sono INFERIORI ai costi totali).
Lo vediamo perché a sinistra della quantità q* (ovvero per quantità inferiori) la curva dei ricavi totali (quella verde) sta al di sotto della curva dei costi totali (quella blu scuro).
Significa che per quelle quantità prodotte e vendute, l’impresa perde.
Abbiamo visto il significato grafico del punto di pareggio.
Adesso andiamo a vedere come si determina analiticamente (cioè partendo dai dati ed usando le formule), per poi mettere tutto insieme in un esempio pratico.
Determinazione analitica del Break Even Point
Per trovare il punto di Break Even, dobbiamo conoscere i costi fissi, i costi variabili e il prezzo del prodotto.
Dati per la determinazione del punto di pareggio
Definiamo nel dettaglio analiticamente come sono composte le rette tracciate nei grafici precedenti.
Costi fissi
Come abbiamo detto, non variano al variare della quantità venduta. Sono una costante.
Li indicheremo con CF.
Costi variabili
Variano al variare della quantità venduta. Li indichiamo con CV.
Indichiamo con cvu il costo variabile unitario (ovvero il costo per ogni unità prodotta).
CV = cvu x q
Costi totali
Sono dati dalla somma tra costi fissi e costi variabili.
Li indichiamo con CT.
CT = CF + CV
Ma sappiamo che CV = cvu x q.
Quindi possiamo scrivere
CT = CF + (cvu x q)
Ricavi totali
Abbiamo già visto che sono dati dal prezzo per il numero di unità prodotte (q).
Li indichiamo con RT.
RT = p x q
Adesso abbiamo tutto quello che ci serve per calcolare il Break Even Point (o punto di pareggio)!
Trovare il punto di pareggio
Sappiamo che il punto di pareggio è il punto in cui i costi totali sono uguali ai ricavi totali.
RT = CT
Sappiamo a cosa equivalgono i ricavi totali e i costi totali. Quindi scriviamo l’uguaglianza esplicitamente, sostituendo a RT e a CT i termini che li caratterizzano.
p x q = CF + (cvu x q)
A questo punto bisogna fare alcune semplici operazioni algebriche (si tratta di una semplicissima equazione di primo grado).
Se alcuni passaggi non sono chiari, potete visitare questo link, che contiene una spiegazione dettagliata delle equazioni di primo grado.
L’incognita è q. Vogliamo sapere quale quantità fa sì che i costi e i ricavi siano uguali.

Siamo quindi arrivati alla quantità di equilibrio.
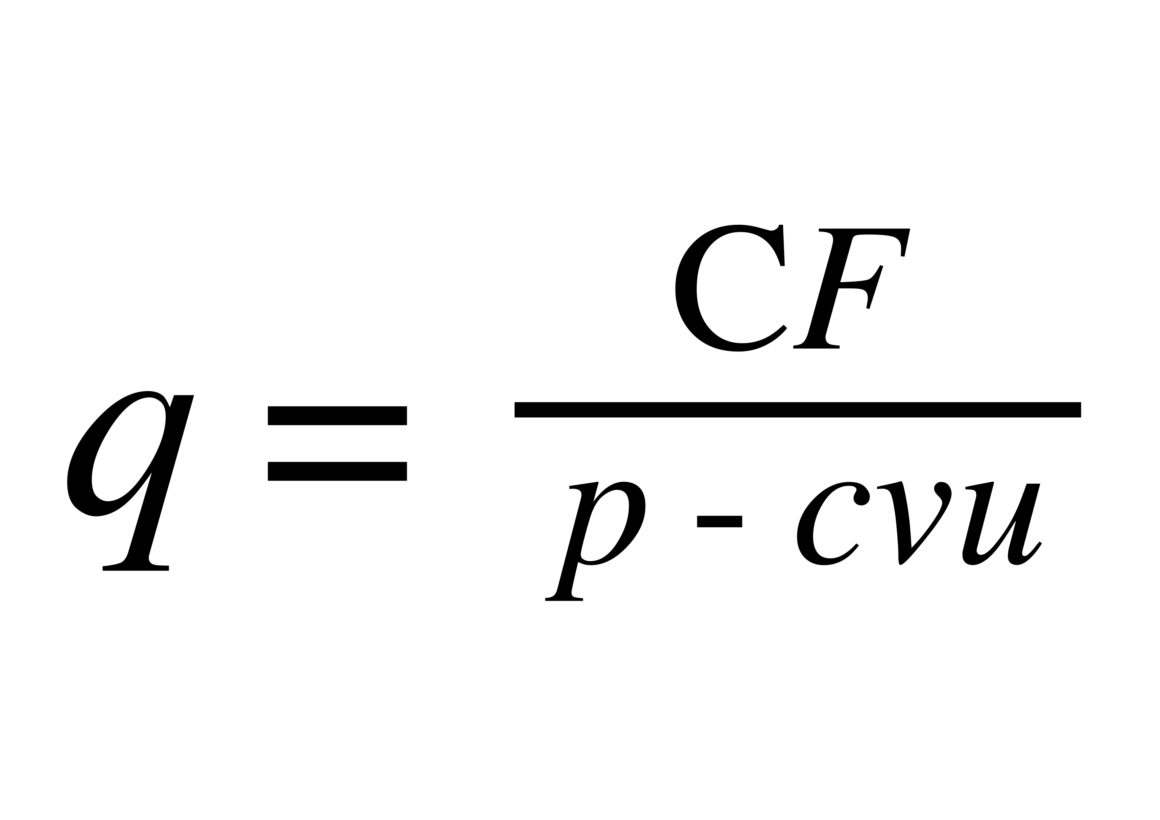
Da qui, si sostituisce la nostra quantità di pareggio (q*)alle formule del ricavo totale e del costo totale, per trovare il costo e il ricevo di pareggio.
Se la quantità prodotta è maggiore della quantità di pareggio, allora l’azienda avrà profitto (area di profitto vista precedentemente).
Mentre se la quantità prodotta è inferiore alla quantità di pareggio, allora l’azienda sarà in perdita (area di perdita, vista anch’essa precedentemente).
Il margine di contribuzione (MdC)
Quello che abbiamo visto al denominatore della quantità di equilibrio è un indice utilissimo in economia aziendale: il margine di contribuzione.
Margine di Contribuzione (MdC) = p – cvu
Esso rappresenta una misura di profitto parziale. In particolare, indica quanta parte del ricavo derivante da un’unità aggiuntiva venduta serva a coprire una parte di costi fissi.
Un’unità aggiuntiva implica il ricavo p (l’azienda incassa il prezzo di quell’unità di prodotto), ma per produrlo, il costo variabile è cvu. Quindi, la parte rimanente (p – cvu)serve a coprire i costi fissi.
Esempi pratici di calcolo del Break Even Point
Per evitare che questo post diventi troppo lungo, gli esempi pratici possono essere consultati in questa pagina:
Vantaggi e svantaggi del modello del punto di pareggio
Il modello di cui abbiamo parlato ha indubbiamente alcuni vantaggi (e anche degli svantaggi che vedremo subito dopo).
Volendo riassumere brevemente i vantaggi del modello, possiamo dire che:
- Il modello aiuta nelle scelte di determinazione del prezzo.
Cambiando il prezzo, cambia anche la pendenza del ricavo totale, e quindi il punto di pareggio si sposta. - Il modello aiuta a capire la struttura di costo dell’impresa.
Ossia, il modello aiuta a delineare meglio quali costi all’interno dell’impresa siano fissi, e quali siano variabili. - È utile per individuare tutti i costi aziendali.
Tuttavia, il modello ha numerosi limiti; in particolare:
- Il modello assume che ci sia una variazione proporzionale dei ricavi, all’aumentare delle vendite.
Il che non è sempre vero. - Tutto ciò che si produce viene venduto.
Il modello non prevede il fatto che la quantità prodotta, potrebbe rimanere in magazzino senza essere venduta (e quindi senza nessun ricavo). - Variazione proporzionale del costo variabile rispetto alla quantità venduta.
I costi (come abbiamo visto nel relativo post)non sempre sono direttamente proporzionali alla quantità prodotta. - Invariabilità dei costi di approvvigionamento al variare della produzione.
È probabile che con quantità prodotte maggiori, l’impresa potrà comprare le materie prime e gli altri fattori della produzione ad un prezzo inferiore. Il modello del break even point non prevede questa eventualità.
Domande e risposte sul Break Even Point
Il Break Even Point (in italiano Punto di Pareggio)è il punto di incontro tra Ricavi Totali e Costi Totali di un’impresa. Indica la quantità che fa si che i costi totali e i ricavi totali dell’impresa siano uguali.
Tuttavia, quando si parla di Break Even Point ci si riferisce spesso non soltanto al punto di per se, ma a tutto il modello che porta alla determinazione di quel punto.
Il BEP serve a capire quale sia la quantità minima da produrre, e se una data quantità sia compatibile con la struttura dei costi dell’impresa e con il prezzo del prodotto.
Inoltre, serve a dare all’impresa informazioni utili per la determinazione del prezzo di prodotto.
Aiuta ad osservare la struttura dei costi dell’impresa, ed ha tanti altri vantaggi, di cui si parla nel post.
In estrema sintesi il punto di pareggio si calcola uguagliando i ricavi totali e i costi totali:
RT = CT
Nel post si vede nel dettaglio come individuarlo sia graficamente che analiticamente.
Alla fine dei calcoli il punto di pareggio è q=CF/(p-cvu)
Il break even point si rappresenta graficamente anzitutto disegnando le curve di costo e di ricavo.
Una volta fatto ciò, il punto di pareggio è il punto di intersezione tra la retta del ricavo totale e quella del costo totale.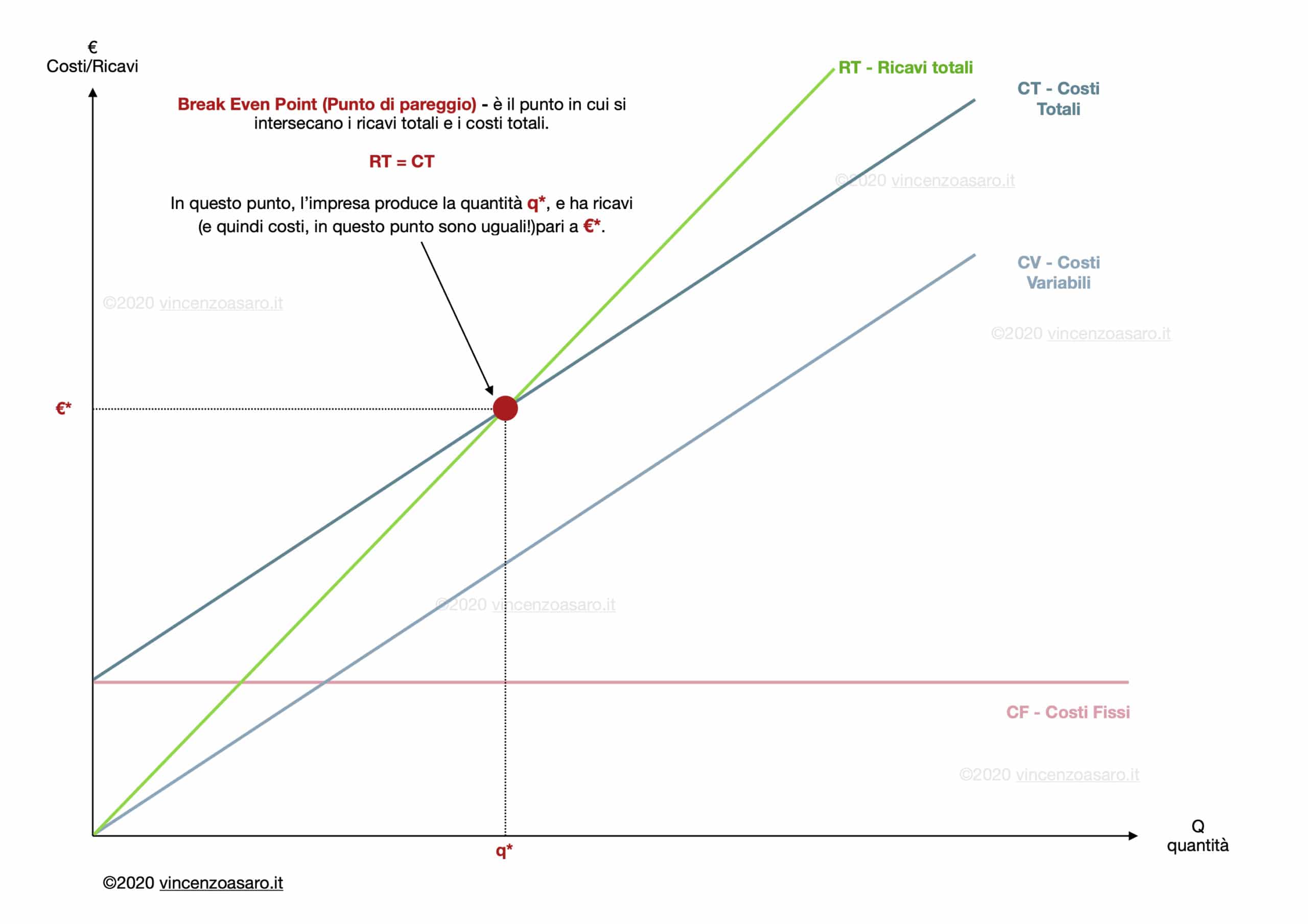
Il margine di contribuzione (MdC) è un indice che permette di determinare quanto un’unità venduta contribuisca alla copertura dei costi fissi.
MdC = p – cvu
dove p è il prezzo del prodotto e cvu indicano i costi variabili unitari.
Puoi trovarli in questo post.
Infografica Break Even Point

Video sul punto di pareggio
Facci sapere cosa ne pensi di questo post valutandolo qui sotto!




