Esercizi svolti sul monopolio – massimizzazione del profitto del monopolista

In questo post raccogliamo alcuni esercizi svolti sul monopolio e sulla massimizzazione del profitto del monopolista.

Il monopolio come forma di mercato è stato già trattato in un post che potete trovare a questo link.

Vedremo alcuni esercizi svolti sul monopolio diversi, che però seguono sempre lo stesso ragionamento: il monopolista massimizza il suo profitto producendo la quantità che rende i ricavi marginali uguali ai costi marginali.

Se siete interessati alla microeconomia potete visitare la pagina dedicata, e anche il canale YouTube, in cui ci sono diversi video sull’argomento.

Esercizio 1 – Esercizio svolto sulla massimizzazione del profitto del monopolista con funzione di domanda inversa e costi totali noti

Un’impresa monopolistica fronteggia una curva di domanda pari a p=1000 – 10Q e costi totali (TC – Total Cost) pari a TC = 100Q.

Determinare (1)la quantità che massimizza il profitto, (2) il prezzo di equilibrio di monopolio e (3)il profitto del monopolista.

Svolgimento esercizio 1

Abbiamo tre punti da svolgere. Iniziamo con il primo.

(1) – Determinare la quantità che massimizza il profitto del monopolista

Anzitutto dobbiamo determinare la quantità che massimizza il profitto del monopolista.

Come sappiamo dal post sul monopolio, il monopolista massimizza il suo profitto quando il ricavo marginale (MR – Marginal Revenue) è uguale al costo marginale (MC – Marginal Cost).

MR = MC

Prima di tutto calcoliamo il ricavo totale (TR – Total Revenue). Conosciamo già il costo totale (TC – Total Cost), dunque deriviamo il ricavo marginale (MR) e il costo marginale (MC), e li eguagliamo.

Il ricavo totale (TR) è dato dal prezzo per la quantità. Il prezzo ce l’abbiamo già (è la funzione di domanda inversa che c’è nel testo dell’esercizio), quindi dobbiamo semplicemente moltiplicarlo per la quantità.

TR = p x Q

Sappiamo che p = 1000 – 10Q

Quindi abbiamo:

Abbiamo trovato il ricavo totale.

Sappiamo già che il costo totale (TC) è 100 Q

TC = 100 x Q

---

Ora dobbiamo calcolare il ricavo marginale (MR)e il costo marginale (MC), e lo facciamo derivando rispettivamente il ricavo totale e il costo totale per la quantità.

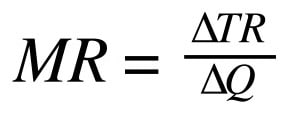
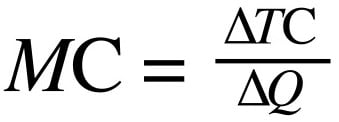
Derivando il nostro ricavo totale (TR)rispetto alla quantità, otteniamo:

MR = 1.000 – 20Q

Come ci aspettavamo, il ricavo marginale ha una pendenza doppia rispetto alla funzione di domanda (p = 1.000 – 10Q).

Lo abbiamo già visto in questo post.

Il nostro costo marginale, ricavato derivando il costo totale rispetto alla quantità, sarà:

MC = 100

Condizione di massimizzazione del profitto del monopolista (MR = MC)

Ricapitolando, abbiamo calcolato il ricavo totale, avevamo già il costo totale.

Derivandoli, abbiamo trovato il costo marginale e il ricavo marginale.

Adesso, dobbiamo uguagliarli, per determinare la quantità che massimizza il profitto del monopolista:

MR = MC

1.000 – 20Q = 100

20Q = 900

Q = 900 / 20

Q = 45

Dunque, la quantità di monopolio, che indichiamo con una m a pedice (Q_m), è 45 unità.

Q_m = 45

Il monopolista, produrrò 45 unità per massimizzare il profitto.

Continuiamo il nostro esercizio svolto sulla massimizzazione del profitto del monopolista con il punto (2), ovvero determinare il prezzo di monopolio.

(2) – Determinare il prezzo di equilibrio di monopolio

Questo secondo punto è molto semplice, dal momento che già nel testo abbiamo già la funzione di domanda in forma inversa.

Sappiamo che p=1000 – 10Q

Abbiamo appena visto che il monopolista produrrà 45 unità per massimizzare il suo profitto (Q_m = 45).

Ci basta sostituire questa quantità alla funzione di domanda inversa, per ottenere il prezzo di monopolio (p_m):

p_m = 1.000 – (10 x 45)

p_m = 1.000 – 450

p_m = 550 €

Il monopolista, fisserà il prezzo a 550 € per unità.

Questo è il prezzo che, data la curva di domanda, gli consente di vendere la quantità che massimizza il suo profitto (45 unità).

Adesso, vediamo qual è il profitto del monopolista, quando vende 45 unità (cioè il profitto massimo). Dunque, andiamo a svolgere il terzo e ultimo punto dell’esercizio.

(3) – Determinare il profitto del monopolista

Sappiamo che il profitto si indica con la lettera greca ‘pi‘ (π), ed è dato dalla differenza tra ricavi totali (TR)e costi totali (TC):

π = TR – TC

Conosciamo già sia i ricavi totali che i costi totali.

TR = 1000 Q – 10 Q²

TC = 100Q

Adesso, dobbiamo sostituire a Q la quantità di monopolio (che è quella che massimizza il profitto del monopolista): Q_m = 45

Facendo i calcoli, otteniamo:

TR = 24.750

TC = 4.500

Quindi il profitto massimizzato del monopolista (π_m)è il seguente:

π_m = 24.750 – 4.500 = 20.250 €

---

Esercizio 2 – Esercizio svolto sulla massimizzazione del profitto del monopolista con costo totale e funzione di domanda diretta noti

Un’impresa sostiene costi totali (TC – Total Costs) rappresentati dalla funzione TC = 0,5Q+5 e si confronta con la funzione di domanda diretta Q=41-2 p

Determinare (1)la quantità che massimizza il profitto del monopolista (Q_m), (2)il prezzo di monopolio (p_m)e (3)il profitto del monopolista.

Svolgimento esercizio 2

Anzitutto, prima di procedere, ci serve la funzione di domanda inversa.

Come sappiamo, la calcoliamo partendo dalla funzione di domanda diretta Q=41-2p

Facendo i calcoli, otteniamo la seguente funzione di domanda inversa:

p = 20,5 – 0,5Q

Adesso che abbiamo la funzione di domanda. informa inversa, procediamo con lo svolgimento dell’esercizio.

(1) – Determinare la quantità che massimizza il profitto di monopolio

Per determinare la quantità che massimizza il profitto di monopolio, dobbiamo eguagliare i ricavi marginali e i costi marginali (condizione di massimizzazione).

I ricavi totali (TR – Total Revenue)sono uguali al prezzo moltiplicato per la quantità.

Il prezzo lo conosciamo (la nostra funzione di domanda inversa, p=20,5 – 0,5Q), ci basta quindi moltiplicarlo per la quantità Q per ottenere i ricavi totali:

TR = p x Q

TR = [20,5 – 0,5Q] x Q

TR = 20,5 Q – 0,5 Q²

Il ricavo marginale, è la derivata del ricavo totale rispetto alla quantità. Derivando il ricavo totale (TR), rispetto alla quantità, otteniamo:

MR = 20,5 – Q

P.S. Avremmo anche potuto ricavare il ricavo marginale partendo dalla funzione di domanda inversa, sapendo che il ricavo marginale ha pendenza doppia rispetto alla curva di domanda. Ci bastava moltiplicare 0,5Q nella funzione di domanda inversa per 2 (il doppio)e avremmo ottenuto lo stesso risultato.

---

Adesso che conosciamo il ricavo marginale, calcoliamo il costo marginale, per poi eguagliarli (condizione di massimizzazione del profitto).

Il costo marginale (MC – Marginal Cost)si calcola derivando il costo totale rispetto alla quantità.

Conosciamo il costo totale dal testo del problema (CT = 0,5Q+5). Derivandolo rispetto alla quantitò, otteniamo il costo marginale:

MC = 0,5

---

Conosciamo adesso sia il ricavo marginale che il costo marginale. Li eguagliamo per trovare la quantità che massimizza il profitto di monopolio:

MR = MC

20,5 – Q = 0,5

Q = 20,5 – 0,5

Q_m = 20

La quantità che massimizza il profitto di monopolio (Q_m – Quantità di monopolio)è 20 unità prodotte.

Qual è il prezzo di monopolio per vendere 20 unità di prodotto? Ce lo dice la curva di domanda.

Andiamo quindi a calcolare il prezzo di monopolio (pm)per vendere la quantità che massimizza il profitto (Q_m=20)

(2) – Determinare il prezzo di monopolio

Per determinare il prezzo di monopolio ci basta sostituire la quantità di monopolio (Q_m = 20, ossia la quantità che rende i ricavi marginali e i costi marginali uguali)alla funzione di domanda inversa.

Sappiamo che la funzione di domanda inversa è:

p = 20,5 – 0,5Q

Ci basta sostituire a Q la quantità Q_m=20, per ottenere il prezzo di monopolio (p_m):

p_m = 20,5 – (0,5 x 20)

p_m = 20,5 – 10

p_m = 10,5 €

Il prezzo di monopolio è 10,5.

Significa che il monopolista (che è price-maker, sceglie il prezzo da applicare)fisserà il prezzo a 10,5 €, perché la curva di domanda gli permette di vendere a questo prezzo 20 unità (ovvero la quantità che gli permette di massimizzare il profitto).

Adesso, l’ultimo punto del problema è determinare il profitto del monopolista.

(3) – Determinare il profitto di monopolio

Il profitto è dato, per definizione, dalla differenza tra i ricavi totali (TR), meno i costi totali (TC).

Sappiamo che per massimizzarlo, il monopolista venderà 20 unità (Q_m=20)al prezzo di 10,5 € ciascuna (p_m=10,5).

π = TR – TC

Conosciamo i ricavi totali:

TR = 20,5 Q – 0,5 Q²

Conosciamo anche i costi totali, che venivano dati nel testo:

TC = 0,5Q+5

Ci basta dunque fare la differenza tra i due, per ottenere il profitto del monopolista. Ovviamente a Q sostituiremo la quantità di monopolio (Q_m=20).

π = TR – TC

π = [20,5 Q – 0,5 Q²] – 0,5Q+5

Sostituiamo a Q la quantità di monopolio (Q_m=20):

π = [(20,5 x 20) – (0,5 x 20²)] – [(0,5×20)+5]

π = [410 – 200] – [10 + 5]

π = 210 – 15

π = 195

Il profitto del monopolista (π)è 195 €.

Esercizio 3 – Esercizi svolti sul monopolio e sulla massimizzazione del profitto del monpolista

La società Monopoly .inc si confronta con una funzione di domanda rappresentata da p=10-y e presenta costi fissi nulli (FC=0)e costi marginali pari ad 1 (MC=1).

Determinare:

1) Quantità e prezzo di monopolio

2) Il profitto del monopolista

Svolgimento esercizio 3

In alcuni esercizi svolti sul monopolio, la quantità non viene indicata con la lettera q, ma con y.

Questo può confondere, ma una volta che si sa che y=q, no dovrebbero esserci problemi.

Per questo, ho lasciato y al posto di q, proprio per abituarvi a questa eventualità.

Iniziamo quindi a risolvere il primo punto dell’esercizio.

(1) – Determinare la quantità e il prezzo di monopolio

Determinare la quantità di monopolio è semplice, e se avete svolto gli esercizi precedenti, dovreste già sapere come si fa.

Sappiamo che il monopolista produce quella quantità che rende i ricavi marginali (MR) uguali ai costi marginali (MC).

Quindi poniamo:

MR = MC

I costi marginali sono uguali ad 1 (come ci viene detto nel problema), mentre sappiamo che i ricavi marginali(MR) sono la derivata dei ricavi totali(TR) rispetto alla quantità.

Quindi calcoliamo i ricavi totali (TR), e poi li deriviamo rispetto alla quantità per ottenere i ricavi marginali (MR)

I ricavi totali sono dati dal prezzo per la quantità (che in questo caso stiamo rappresentando con y, non con q).

TR = p x y

Come vediamo nel testo del problema, p=10-y (funzione di domanda inversa), quindi:

TR = (10 – y) x y

Svolgendo i calcoli otteniamo:

TR = 10y – y_²

Ora che abbiamo i ricavi totali, dobbiamo semplicemente derivarli rispetto alla quantità (y), per ottenere i ricavi marginali.

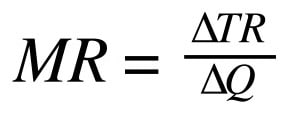
Derivando i ricavi totali (TR)rispetto alla quantità (y)otteniamo i ricavi marginali (MR):

MR = 10-2y

Adesso, poniamo i ricavi marginali (MR)uguali ai costi marginali (MC)per ottenere la quantità di monopolio (y_m):

MR = MC

10-2y = 1

2y = 9

y_m = 9/2

Il monopolista produce la quantità di 9/2.

A quale prezzo?

Ci basta sostituire questa quantità alla funzione di domanda inversa (p=10-y)per conoscere il prezzo di monopolio (p_m).

p = 10 – y

p = 10 – 9/2

p_m = 11/2

Il prezzo di monopolio (p_m), quindi, è pari a 5,5 € (11/2).

Abbiamo risposto al primo quesito, trovando quantità (y_m)e prezzo(p_m)di monopolio.

Possiamo passare al secondo quesito, che ci chiede di determinare il profitto del monopolista.

(2) – Determinare il profitto del monopolista

Come sappiamo, il profitto (π)è dato dalla differenza tra ricavi totali (TR)e costi totali (TC):

π = TR – TC

Conosciamo i ricavi totali (li abbiamo calcolati nel punto precedente: TR = 10y – y_²)e sappiamo che i costi totali sono dati dalla somma tra costi fissi (FC)e costi variabili (VC). Dal momento che i costi fissi sono nulli (FC = 0), l’unico costo variabile è quello marginale, pari a 1, per la quantità prodotta (y_m)

TC = MC x y_m

TC = 1 x 9/2

TC = 9/2

Dunque:

π = TR – TC

π = 10y – y_² – 9/2

π = (10 x 9/2) – (9/2)² – 9/2

π = 45 – 81/4 – 9/2

π = (180 – 81 – 18)/4

π = 81/4

π = 20,25 €

Il profitto del monopolista è pari a 20,25 €.