Come calcolare la mediana di una distribuzione in classi?
Abbiamo già parlato nel dettaglio della mediana in un post dedicato, accennando al calcolo della mediana di una distribuzione in classi.
In questo post, vedremo passo per passo in che modo si calcola la mediana di una distribuzione in classi, e potrei vedremo l’applicazione pratica con un esempio.
Come calcolare la mediana di una distribuzione in classi?
Dobbiamo fare semplicemente due cose:
- Trovare la classe mediana
- Determinare la mediana (o valore mediano).
CALCOLARE LA MEDIANA DI UNA DISTRIBUZIONE IN CLASSI
Come si trova la classe mediana?
Per trovare la classe mediana, dobbiamo semplicemente dividere il numero totale di osservazioni (n)per due.
La classe la cui frequenza cumulata è in corrispondenza di n/2 sarà la nostra classe mediana.
Se sembra confusionario, non preoccupatevi. Tutto sarà chiaro con un esempio che vedremo tra un attimo.
Una volta determinata la classe mediana, rimane soltanto da calcolare la mediana (il valore mediano).
Determinare la mediana (o valore mediano) – Metodo dell’interpolazione
Per calcolare la mediana (valore mediano)una volta che si è determinata la classe mediana, si applica un metodo, detto “metodo dell’interpolazione”.
Basta applicare la seguente formula:
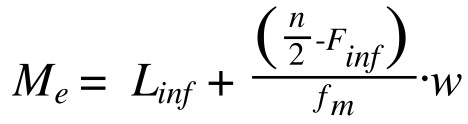
Dove:
Linf è il limite inferiore della classe mediana.
fm è la frequenza assoluta della classe mediana.
n è il numero di osservazioni totali.
Finf è la frequenza cumulata della classe precedente a quella mediana (ovvero la somma delle frequenze assolute delle classi precedenti a quella mediana).
w è l’ampiezza della classe mediana.
Proviamo a vedere come si calcola la mediana di una distribuzione per classi con un esempio pratico, che dovrebbe rendere tutto più comprensibile.
Esempio di calcolo della mediana di una distribuzione in classi
La seguente tabella riassume il consumo in kw di un piccolo comune rilevato per 300 giorni:
| Consumo giornaliero (in kw) | Giorni (frequenza assoluta) |
|---|---|
| 0 – 99 | 50 |
| 100 – 199 | 85 |
| 200 – 399 | 65 |
| 400 – 599 | 55 |
| 600 – 1000 | 45 |
| Totale (n) | 300 |
Calcoliamo la mediana di questa distribuzione in classi.
ESEMPIO DI CALCOLO DELLA MEDIANA DI UNA DISTRIBUZIONE IN CLASSI
Calcoliamo le frequenze cumulate
Iniziamo anzitutto col calcolare le frequenze cumulate, perché questo ci aiuterà ad identificare la classe mediana.
La distribuzione ci dice che per 50 giorni, si sono consumati tra gli 0 e i 99 kw nel comune. Per 85 giorni si sono consumati tra i 100 e i 199 kw, e così via.
| Consumo giornaliero (in kw) | Giorni (frequenza assoluta) | Frequenza cumulata |
|---|---|---|
| 0 – 99 | 50 | 50 |
| 100 – 199 | 85 | 135 |
| 200 – 399 | 65 | 200 |
| 400 – 599 | 55 | 255 |
| 600 – 1000 | 45 | 300 |
| TOTALE(n) | 300 |
ESEMPIO DI CALCOLO DELLA MEDIANA DI UNA DISTRIBUZIONE IN CLASSI
1. Trovare la classe mediana
Adesso che abbiamo ordinato e calcolato le frequenze cumulate, dobbiamo trovare la classe mediana.
Lo facciamo dividendo il numero totale di osservazioni (n)per due.
Sappiamo che n=300.
n/2 = 300/2 = 150
La classe mediana è quella in posizione 150
Come vediamo dalle frequenze cumulate, la classe in posizione 150 è la classe 200-399 (questo perché 150 è compreso tra 135 e 200 (le frequenze cumulate nella seconda e nella terza riga della tabella superiore).
150 è più di 135, ma meno di 200. Dunque la classe mediana è quella in corrispondenza della frequenza cumulata di 200. La classe 200-399.
Abbiamo trovato la classe mediana. Come facciamo a trovare la mediana?
ESEMPIO DI CALCOLO DELLA MEDIANA DI UNA DISTRIBUZIONE IN CLASSI
2. Calcolare la mediana di una distribuzione in classi
Come abbiamo detto, per il calcolo usiamo un semplice metodo (detto metodo dell’interpolazione), che consiste nell’applicare la formula che abbiamo già visto:
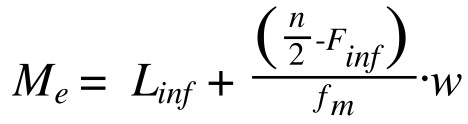
Nel nostro esempio, il limite inferiore della classe mediana (Linf) è 200 (ricordiamo che la classe mediana è 200-399). La frequenza assoluta della classe mediana (fm) è 65. Il numero di osservazioni totali (n)è 300, e la frequenza cumulata della classe precedente a quella mediana (Finf) è 135.
L’ampiezza della classe mediana (2)è 199.
È dato da 399 – 200 = 199.
Applicando la formula con questi dati otteniamo:
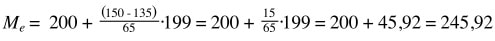
La mediana, dunque, è 245,92.
Non c’è altro che si debba fare.
Per approfondire, potete anche visitare il post dedicato alla mediana, e potete trovare tanti altri post sulla statistica nella pagina dedicata, e diversi video nel canale YouTube.