Frequenze cumulate: un concetto fondamentale per interpretare i dati in modo chiaro ed efficace. Se vuoi padroneggiare la statistica e affinare le tue capacità analitiche, questo articolo ti guiderà attraverso uno strumento essenziale per l’economia e la finanza.
Per parlare dell’argomento, partiremo da un esempio per poi passare alla definizione formale
Esempio
Osserviamo la seguente tabella:
| Nome | Altezza (in cm) |
| Francesca | 164 |
| Giorgio | 176 |
| Laura | 166 |
| Pietro | 174 |
| Filippo | 172 |
| Ada | 164 |
| Giovanna | 166 |
| Luca | 172 |
| Rossana | 166 |
| Mario | 174 |
La tabella riassume il carattere “Altezza in cm” di una classe di dieci studenti.
Quella che vediamo è detta distribuzione unitaria semplice, ossia una semplice lista delle nostre osservazioni.
Nella colonna di sinistra vediamo il nome degli alunni, e nella colonna di destra vediamo l’altezza in centimetri.
Notiamo che abbiamo usato dei dati quantitativi. Questo perché:
Le frequenze cumulate si possono calcolare solo su caratteri quantitativi oppure su caratteri qualitativi ordinali.
In altre parole, possono essere calcolate soltanto su caratteri che possono essere messi in ordine dal più piccolo al più grande.
Fatta questa piccola digressione, torniamo al nostro esempio.
Trasformiamo questa distribuzione unitaria semplice in una distribuzione di frequenze, dove a sinistra metteremo le varie modalità osservate (cioè le altezze in centimetri), e a destra la frequenza assoluta.
La tabella che otterremo è la seguente:
| Modalità (xi) | Frequenze assolute (ni) |
| 164 | 2 |
| 166 | 3 |
| 172 | 2 |
| 174 | 2 |
| 176 | 1 |
Abbiamo la nostra distribuzione di frequenze. Fin qui niente di nuovo.
Adesso, poniamoci una domanda:
Quanti ragazzi sono più bassi di un 175 centimetri?
Una opzione è contare, e sappiamo già che sono 9 (soltanto uno è più alto).
Dato che questa distribuzione di frequenze è soltanto un esempio, è semplice contare. Ma immaginiamo una distribuzione di frequenze con migliaia di modalità. La faccenda diventa più complicata.
Per questo ci tornano utili le frequenze cumulate.
Una frequenza cumulata è una somma. Ovvero la somma della frequenza della modalità presa in considerazione, e delle frequenze precedenti.
La prima modalità osservata nella nostra tabella è 164, e la frequenza assoluta è 2 (significa che due ragazzi nella classe sono alti 164 centimetri).
La frequenza cumulata della modalità 164 sarà 2, in quanto non ci sono modalità “precedenti” (cioè inferiori).
Aggiungiamo una colonna alla nostra distribuzione di frequenze, in cui indichiamo la frequenza cumulata della prima modalità (164).
Solitamente, le frequenze cumulate si indicano con Ni, con la N maiuscola (al contrario delle frequenze assolute, che si indicano con ni).
| Modalità (xi) | Frequenze assolute (ni) | Frequenze cumulate (Ni) |
| 164 | 2 | 2 |
| 166 | 3 | |
| 172 | 2 | |
| 174 | 2 | |
| 176 | 1 | |
| TOTALE | 10 |
Adesso ti faccio una domanda, e ti chiedo di perdere qualche secondo provando a rispondere prima di continuare a leggere:
Qual è la frequenza cumulata della modalità 166?
La risposta è:
5
Come abbiamo detto, la frequenza cumulata è la somma della frequenza assoluta della modalità osservata e di quelle precedenti.
La modalità osservata in questo caso è 166, e la sua frequenza assoluta è 3.
C’è soltanto una modalità “precedente” (quindi più piccola), ovvero 164, e la sua frequenza assoluta è 2.
Quindi la frequenza cumulata è data dalla somma della frequenza assoluta della modalità 166 (3) e la somma della frequenza assoluta della modalità precedente, la modalità 164 (la cui frequenza assoluta è 2.
Dunque inseriamo anche questa frequenza cumulata nella nostra tabella.
| Modalità (xi) | Frequenze assolute (ni) | Frequenze cumulate (Ni) |
| 164 | 2 | 2 |
| 166 | 3 | 5 |
| 172 | 2 | |
| 174 | 2 | |
| 176 | 1 | |
| TOTALE | 10 |
Adesso riportiamo la tabella con tutte le frequenze cumulate. Prova a calcolarle tu, prima di continuare a leggere.
| Modalità (xi) | Frequenze assolute (ni) | Frequenze cumulate (Ni) |
| 164 | 2 | 2 |
| 166 | 3 | 5 |
| 172 | 2 | 7 |
| 174 | 2 | 9 |
| 176 | 1 | 10 |
| TOTALE | 10 |
Notiamo che la frequenza cumulata dell’ultima modalità (176)è uguale al totale delle osservazioni, cioè 10 (i dieci alunni della classe).
In questo esempio, quindi, abbiamo visto cosa siano le frequenze cumulate: una semplice somma.
Diamone una definizione più completa.
Definizione di frequenze cumulate
La frequenza cumulata di una modalità (o di una classe di modalità)è pari alla somma della frequenza assoluta della modalità (o classe)e delle frequenze assolute delle modalità che la precedono.
Di solito, le frequenze cumulate vengono rappresentate con Ni (n maiuscola).
Possiamo inserire la frequenza cumulata in una rappresentazione formale di una distribuzione di frequenza come segue:
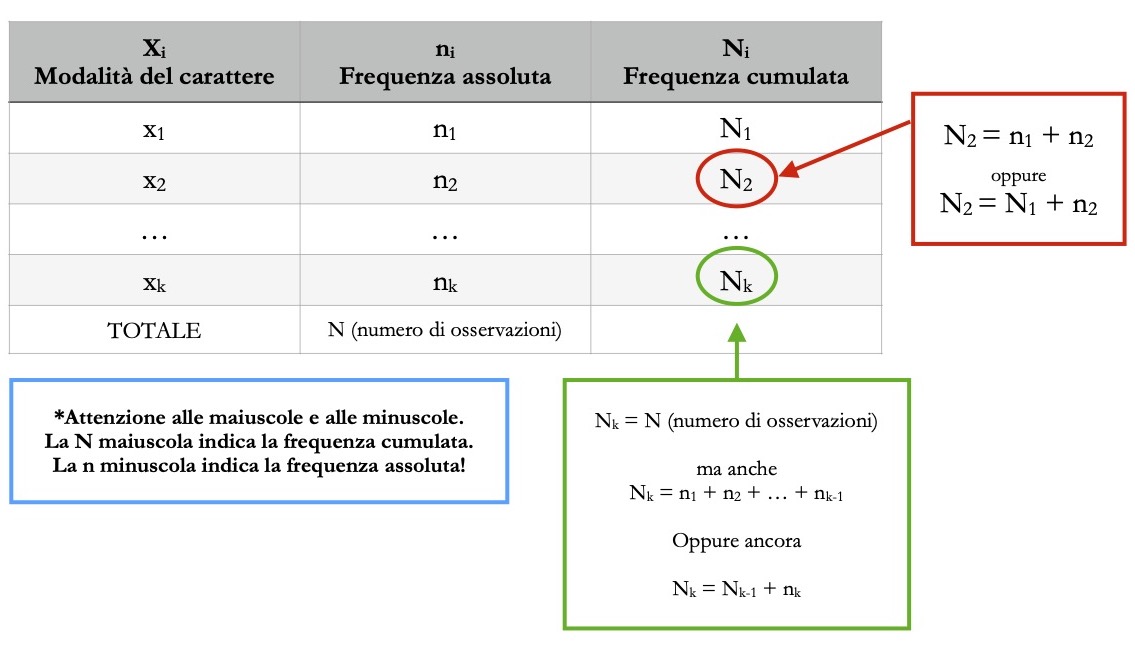
Finora abbiamo parlato delle frequenze assolute cumulate, ma si possono calcolare anche altri tipi di frequenze cumulate.
Frequenze relative cumulate e frequenze percentuali cumulate
Finora abbiamo parlato delle frequenze assolute cumulate, ma si possono calcolare anche altri tipi di frequenze cumulate.
Abbiamo parlato in dei post specifici sia delle frequenze relative, che di quelle percentuali.
Si possono calcolare le frequenze cumulate anche sulle frequenze relative e sulle frequenze percentuali. Il principio è sempre lo stesso.
Nel caso di frequenze relative, dobbiamo sommare la frequenza relativa osservata, e tutte le frequenze relative precedenti.
Riprendiamo il nostro esempio dei dieci alunni, e includiamo anche le frequenze relative:
| Modalità (xi) | Frequenze assolute (ni) | Frequenze relative (fi) |
| 164 | 2 | 0,2 |
| 166 | 3 | 0,3 |
| 172 | 2 | 0,2 |
| 174 | 2 | 0,2 |
| 176 | 1 | 0,1 |
| TOTALE | 10 | 1 |
Adesso, calcoliamo le frequenze relative cumulate, così come avevamo fatto con le frequenze assolute.
Indichiamo le frequenze relative cumulate con Fi (la F è maiuscola), mentre le frequenze relative sono indicate con fi (la f è minuscola).
| Modalità (xi) | Frequenze assolute (ni) | Frequenze relative (fi) | Frequenze relaive cumulate (Fi) |
| 164 | 2 | 0,2 | 0,2 |
| 166 | 3 | 0,3 | 0,5 |
| 172 | 2 | 0,2 | 0,7 |
| 174 | 2 | 0,2 | 0,9 |
| 176 | 1 | 0,1 | 1 |
| TOTALE | 10 | 1 |
La stessa cosa vale anche per le frequenze percentuali. Per calcolare la frequenza percentuale cumulata di una modalità, basta sommare la frequenza percentuale di quella modalità, e tutte le frequenze percentuali precedenti.
Per qualsiasi domanda o richiesta, non esitate a contattarmi!
Facci sapere se questo post ti è stato utile lasciando una valutazione qui sotto!




Fin’ora non ho mai visto spiegazioni più chiaro di questo. Grazie davvero!
E un professore bravissimo
Grazie Marilena! Non sono un professore, ma sono felice se ti sono stato d’aiuto!
Finalmente ho capito uttavia pur comprendendo il calcolo matematico …che cosa serve la frequenza cumulative o meglio cosa ci fornisce? Grazie mille
Ciao! Sono felice che il post ti sia stato d’aiuto.
In breve, le frequenze cumulate ci servono per “semplificarci la vita”. Immagina di avere una distribuzione di frequenze in cui sono inclusi i redditi delle famiglie italiane.
Adesso immagina di voler sapere quante famiglie hanno un reddito inferiore di 20.000 € (è soltanto un esempio).
Con le frequenze cumulate, puoi vederlo immediatamente, senza dover fare altri calcoli.
Questo è soltanto un esempio pratico per farti vedere a cosa possono servire!
Se qualcosa non dovesse essere chiaro, ,chiedi pure!