Le frequenze relative e assolute sono concetti fondamentali quando si parla di statistica e distribuzioni dei dati. In questo post, esploreremo insieme le frequenze relative, un aspetto cruciale per comprendere come i dati si distribuiscono e si confrontano tra loro.
Se hai bisogno di una panoramica completa su distribuzioni unitarie semplici e distribuzioni di frequenza, ti consiglio di dare un’occhiata al nostro post dedicato a questi temi. Sarà un ottimo punto di partenza per approfondire l’argomento.
Alla fine della pagina troverai anche un video esplicativo, tratto dal nostro canale YouTube, che ti guiderà passo passo nella comprensione del concetto.
Per ora, ci concentreremo solo sul significato di frequenze relative, senza entrare troppo nei dettagli su quando è il momento giusto per calcolarle. Tuttavia, è importante sapere che in molte situazioni statistiche, conoscere le frequenze relative è non solo utile, ma spesso indispensabile per analizzare i dati in modo accurato e significativo.
Le frequenze assolute (richiamo)
Facciamo un breve richiamo di quanto abbiamo visto nel post sulla distribuzione di frequenze, perché è necessario per comprendere le frequenze relative.
La frequenza assoluta risponde alla domanda:
quante volte (quanto di frequente)abbiamo osservato ogni modalità assunta da un carattere?
Ipotizziamo di osservare il carattere “colore degli occhi” in una classe di dieci alunni.
La seguente distribuzione di frequenze (assolute)riassume le nostre rilevazioni:
| Colore degli occhi | Frequenza assoluta |
| Blu | 2 |
| Marroni | 4 |
| Verdi | 4 |
| TOTALE | 10 |
La tabella ci dice che nella nostra classe ci sono due alunni con gli occhi blu, quattro con gli occhi marroni, e quattro con gli occhi verdi.
Queste sono le frequenze assolute.
Proviamo a calcolare le frequenze relative sulla stessa distribuzione. Prima di farlo, però, prendiamoci una “pausa” e definiamo cosa sono le frequenze relative.
Torneremo a questo esempio sul colore degli occhi subito dopo.
Cosa sono le frequenze relative
Una frequenza relativa è definita come il rapporto tra la frequenza assoluta e il totale delle osservazioni.

Vediamolo prima in forma generica e poi con un esempio che chiarirà tutto.
In generale, una distribuzione di frequenze assolute è rappresentata come segue:
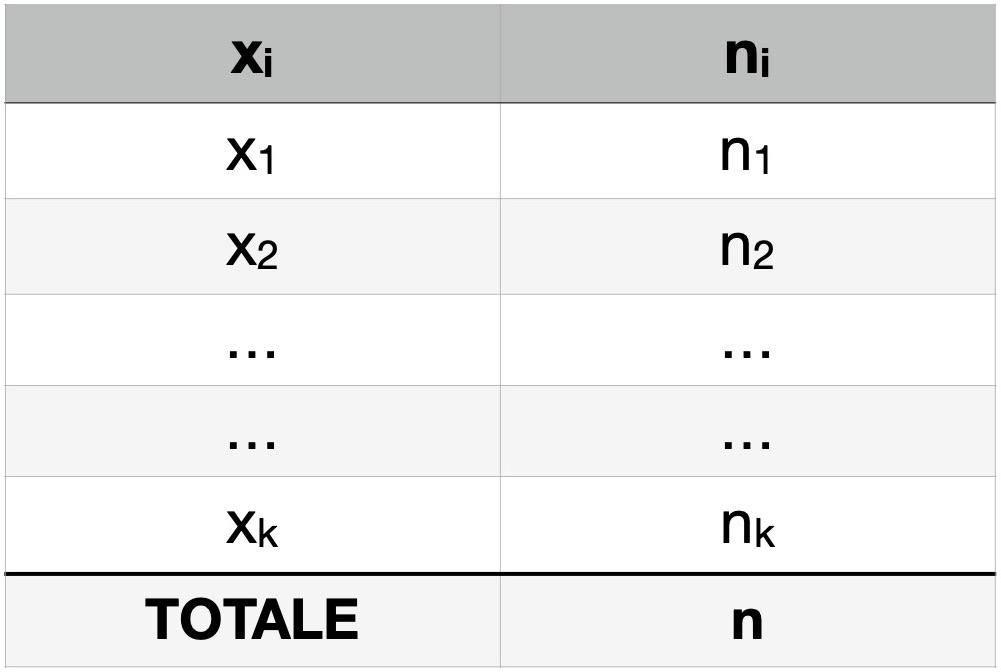
Nella tabella, x è il carattere osservato.
x1, x2, …, xk sono le varie modalità del carattere.
n1, n2, …, nk sono le frequenze assolute.
n è il numero totale delle osservazioni (ed è, ovviamente, la somma n1+n2+…+nk)
Partendo dalle frequenze assolute, calcoliamo le frequenze relative.
In particolare, indicheremo le frequenze relative con fi e le definiamo come segue:
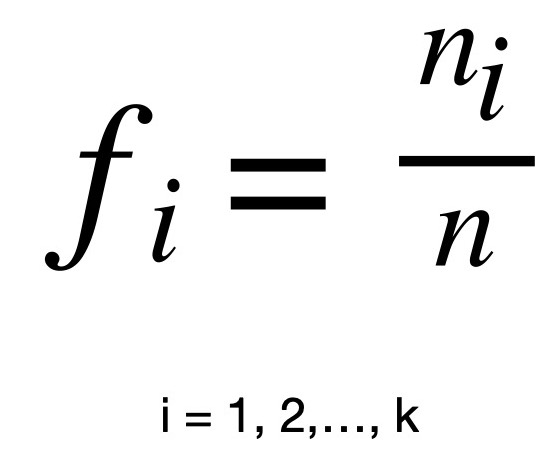
Questo è semplicemente il modo formale di rappresentare le frequenze relative. Ovvero come il rapporto tra la frequenza assoluta di una modalità (ni), e il totale delle osservazioni effettuate (n).
Ad esempio, se una modalità viene osservata 10 volte, in un collettivo di 100 persone, la frequenza relativa sarà semplicemente la divisione 10/100, ovvero 0,1.
Se qualcosa dovesse sembrare complicato al momento, è normale. Quando si rappresentano le cose in modo formale la confusione è sempre presente, ma quando faremo un semplice esempio, tutto tornerà semplice e comprensibile!
La somma delle frequenze relative è uno!
Una cosa da notare è che la somma di tutte le frequenze relative è uno. Formalmente, lo rappresentiamo così:

Tornando alla tabella precedente (quella delle frequenze assolute), possiamo affiancare un’ulteriore colonna, nella quale riportiamo le varie frequenze relative, come nel modo seguente:
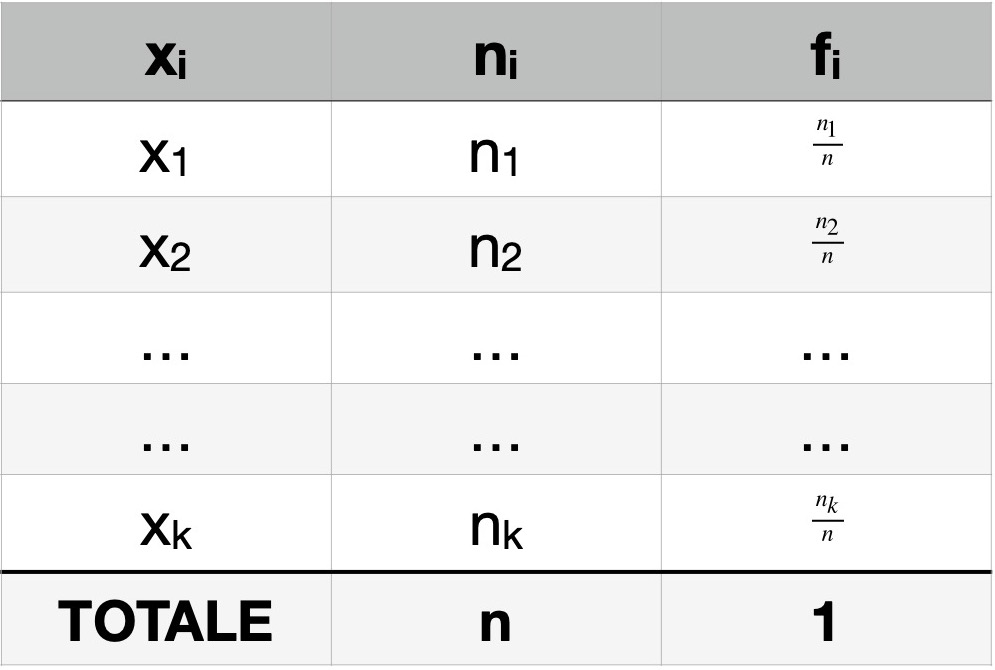
Notiamo nell’ultima riga della tabella che la somma totale delle frequenze assolute è n (ovvero il numero di osservazioni)mentre la somma totale delle frequenze relative è 1 (come abbiamo appena detto).
Adesso andiamo a vedere un semplice esempio che dovrebbe rendere tutto estremamente più chiaro.
Esempio – Calcolare le frequenze relative partendo dalle frequenze assolute
Come promesso all’inizio del post, facciamo un esempio semplicissimo di calcolo delle frequenze relative, sulla tabella che riassume i colori degli occhi di una classe di 10 alunni.
Riportiamo la tabella qui:
| Colore degli occhi | Frequenza assoluta |
| Blu | 2 |
| Marroni | 4 |
| Verdi | 4 |
| TOTALE | 10 |
Nella colonna di destra della tabella, abbiamo le frequenze assolute, e sappiamo che il numero di osservazioni è 10, cioé il numero di alunni nella classe (n=10).
Nella colonna di sinistra abbiamo le diverse modalità assunte dal carattere “colore degli occhi”, ovvero ‘Blu’, ‘Marroni’, e ‘Verdi’.
Adesso ti faccio una domanda, e vorrei che ti fermassi a ragionarci un attimo prima di continuare a leggere. La domanda è la seguente:
Qual è la frequenza relativa della modalità ‘Blu’?
Prenditi un paio di minuti per pensarci e poi continuate per dare la tua risposta!
Come abbiamo ormai ripetuto più volte, per calcolare la frequenza relativa dobbiamo dividere la frequenza assoluta della modalità osservata, per il numero di osservazioni totali.
Stiamo osservando la modalità “Blu” e la sua frequenza assoluta è 2.
Il numero di osservazioni totali (n)è 10.
Dobbiamo quindi semplicemente effettuare la divisione 2:10, e otterremo 0,2!
La frequenza relativa della modalità ‘Blu’ è 0,2
Complimenti se hai risposto correttamente!
Se invece hai sbagliato, non preoccuparti, c’è il tempo per recuperare. Adesso ti chiedo di disegnare questa tabella:
| Colore degli occhi | Frequenza assoluta | Frequenza relativa |
| Blu | 2 | 0,2 |
| Marroni | 4 | |
| Verdi | 4 | |
| TOTALE | 10 |
La prima frequenza relativa, è 0,2.
Ti chiedo di fermarti e calcolare le altre due frequenze relative prima di continuare a leggere. Puoi scrivere le frequenze relative nell’apposita colonna, e confrontarle con le risposte.
Se hai effettuato i calcoli correttamente, la vostra tabella dovrebbe essere come questa (cliccaci sul pulsante per vederla):
| Colore degli occhi | Frequenza assoluta | Frequenza relativa |
| Blu | 2 | 0,2 |
| Marroni | 4 | 0,4 |
| Verdi | 4 | 0,4 |
| TOTALE | 10 |
Le frequenze relativa delle modalità “Marroni” e “Verdi” sono uguali perché anche le frequenze assolute sono le stesse.
Ho lasciato la riga del totale vuota, proprio per farvi notare che, se avete effettuato i calcoli correttamente, la somma delle frequenze relative deve necessariamente essere uno!
Ecco quindi di seguito la tabella completa:
| Colore degli occhi | Frequenza assoluta | Frequenza relativa |
| Blu | 2 | 0,2 |
| Marroni | 4 | 0,4 |
| Verdi | 4 | 0,4 |
| TOTALE | 10 | 1 |
Frequenze relative e confronto di due collettivi
Una cosa da tenere in considerazione è che le frequenze relative non presentano un inconveniente che invece è proprio delle frequenze assolute.
All’aumentare delle dimensioni del collettivo osservato, aumenteranno inevitabilmente anche le frequenze assolute.
Confrontando quindi due collettivi, di cui uno molto più grande dell’altro, indubbiamente le frequenze assolute del collettivo più grande saranno di gran lunga maggiori di quelle del collettivo di minor dimensione.
Questo può rendere difficile il confronto di due collettivi di dimensioni molto diverse, e per ovviare a questo problema si possono usare le frequenze relative.
Prendiamo come esempio la nostra classe di 10 alunni, e ipotizziamo di volerlo confrontare con un’altro collettivo (un istituto di 1000 alunni in cui per semplicità tutti hanno soltanto occhi blu, verdi e marroni).
Otteniamo le seguenti distribuzioni di frequenze assolute:
| Colore degli occhi | Frequenza assoluta |
| Blu | 2 |
| Marroni | 4 |
| Verdi | 4 |
| TOTALE | 10 |
| Colore degli occhi | Frequenza assoluta |
| Blu | 250 |
| Marroni | 400 |
| Verdi | 350 |
| TOTALE | 1000 |
Come vediamo, mettere a confronto questi due collettivi è difficile, perché le frequenze assolute non si possono comparare.
Ad esempio, se volessimo sapere in quale collettivo il tasso di ragazzi con gli occhi blu è maggiore, la comparazione non risulta agevole.
Proviamo ad aggiungere le frequenze relative per entrambi i collettivi, e vedremo che la comparazione risulterà più semplice:
| Colore degli occhi | Frequenza assoluta | Freq. relativa |
| Blu | 2 | 0,2 |
| Marroni | 4 | 0,4 |
| Verdi | 4 | 0,4 |
| TOTALE | 10 | 1 |
| Colore degli occhi | Frequenza assoluta | Freq. relativa |
| Blu | 250 | 0,25 |
| Marroni | 400 | 0,4 |
| Verdi | 350 | 0,35 |
| TOTALE | 1000 | 1 |
Notiamo come in questo caso, osservando le frequenze relative, la comparazione dei due collettivi risulti più semplice.
Ricapitolando
Abbiamo visto cosa sono le frequenze assolute, e abbiamo visto che partendo da queste, si possono calcolare le frequenze relative.
Una frequenza relativa è definita dal rapporto tra la frequenza assoluta della modalità osservata e il numero di osservazioni.
Questa definizione è stata prima enunciata formalmente, e poi messa in pratica con un breve esempio di calcolo delle frequenze relative.
Se hai qualche dubbio, o qualcosa non dovesse essere chiaro, non esitare a contattarmi!
Video sulle frequenze relative
Domande e risposte
È definita come il rapporto tra la frequenza assoluta e il totale delle osservazioni.
La somma delle frequenze relative in una distribuzione deve essere necessariamente uno.
Facci sapere cosa ne pensi di questo articolo valutandolo qui sotto!




