Il dilemma del prigioniero è uno dei giochi più famosi della teoria dei giochi: un rompicapo strategico non cooperativo che mette alla prova la razionalità e le scelte degli individui. Ideato dal matematico canadese Albert Tucker e sviluppato nel tempo, ha trovato applicazioni in tantissimi ambiti, tra cui l’economia.
La teoria dei giochi può sembrare un labirinto complesso, ma oggi la affrontiamo con un approccio semplice e pratico. Vedremo come il comportamento di due “giocatori” cambia quando si trovano in una situazione strategica, ovvero quando le loro scelte si influenzano a vicenda.
Se vuoi approfondire, scorri fino in fondo: troverai un video dedicato che ti guiderà passo dopo passo nel ragionamento dietro questo affascinante gioco.
Abbiamo già toccato questo tema nel nostro post sull’oligopolio, ma qui ci concentreremo su come funziona il dilemma del prigioniero e perché è così importante in economia (e non solo!).
- Cos'è un gioco ad informazione completa?
- Perché in economia ci interessa il dilemma del prigioniero?
- Un esempio di dilemma del prigioniero
- La strategia dominante: che scelta faranno Mario e Adele?
- Il paradosso del dilemma del prigioniero
- Evitare che si confessi: introdurre minacce credibili
- Video sul dilemma del prigioniero
Cos’è un gioco ad informazione completa?
Nella teoria dei giochi, una situazione è a informazione completa quando tutti i giocatori sanno esattamente con chi hanno a che fare. In altre parole, ogni partecipante ha accesso a tutte le informazioni rilevanti sugli altri.
In particolare, ogni giocatore conosce:
- Le possibili strategie che gli altri possono adottare
- L’utilità (o il valore) che ogni scelta ha per gli altri giocatori
Questo significa che nessuno gioca al buio: tutti sanno quali mosse sono sul tavolo e quanto valgono per gli avversari. Ma attenzione: sapere tutto non significa prevedere tutto… e qui sta il bello della strategia!
Perché in economia ci interessa il dilemma del prigioniero?
Il dilemma del prigioniero non è solo un esperimento teorico: può aiutarci a capire come si comportano le imprese quando si trovano in situazioni strategiche. In altre parole, quando le decisioni di un’azienda dipendono dalle mosse della concorrenza… e viceversa!
Ogni impresa deve scegliere se collaborare, competere o persino bluffare, sapendo che ogni azione avrà conseguenze dirette sul mercato e sugli altri giocatori. Ecco perché il dilemma del prigioniero è così utile per analizzare le dinamiche economiche e le strategie aziendali!
Un esempio di dilemma del prigioniero
Due rapinatori: Mario e Adele
Passiamo all’argomento di questo post. Ipotizziamo di avere due rapinatori: Mario e Adele, che hanno appena rapinato una grossa banca.
Mario e Adele si erano promessi che, se fossero stati interrogati dalla polizia, non avrebbero confessato.

La polizia scopre i due rapinatori ma non ha prove sufficienti a condannarli
La polizia dopo qualche indagine arriva a Mario e Adele, ma non ha le prove necessarie per farli condannare. L’unico modo per ottenere una condanna è farli confessare.
Se la polizia riesce a dimostrare che i due sono colpevoli, può condannarli a 4 anni di carcere ciascuno.
Voi direte: è impossibile, i due si erano promessi di non collaborare con la polizia.
Ma la polizia ha un paio di armi: anzitutto conosce il dilemma del prigioniero, e in secondo luogo ha delle prove per reati minori commessi dai due, che bastano per mandarli in galera per un anno ciascuno.

La polizia conosce il dilemma del prigioniero
A questo punto la polizia, che come abbiamo detto conosce la teoria dei giochi, decide di metterla in pratica, interrogando separatamente Mario e Adele.
L’interrogatorio di Mario
La polizia spiega a Mario che non hanno le prove per condannarlo, ma che comunque hanno le prove di altri reati minori, quindi anche se sta zitto, possono metterlo dentro per un anno.
Dunque prospettano a Mario le conseguenze delle due scelte che ha:
- Se Mario confessa e Adele sta zitta, a Mario viene abbuonato l’anno di carcere che dovrebbe scontare, e Adele prenderà 10 anni.
Se invece anche Adele confessa, prenderanno 4 anni ciascuno. - Se Mario sta zitto e anche Adele sta zitta, prenderanno un anno ciascuno. Ma se invece Adele confessa, mentre mario no, allora Mario prenderà 10 anni, e Adele zero.
La proposta della polizia a Mario è riassunta in questa immagine:

L’interrogatorio di Adele
Ad Adele la polizia fa lo stesso discorso, a parti invertite. Ecco cosa le dice:

Nota: il gioco è a informazione completa, quindi Mario sa ciò che la polizia ha detto ad Adele, e viceversa.
La strategia dominante: che scelta faranno Mario e Adele?
A questo punto possiamo disegnare la cosiddetta matrice dei payoff, che è semplicemente una tabella in cui indichiamo le possibili strategie di Mario e Adele, e le conseguenze delle strategie da loro adottate.
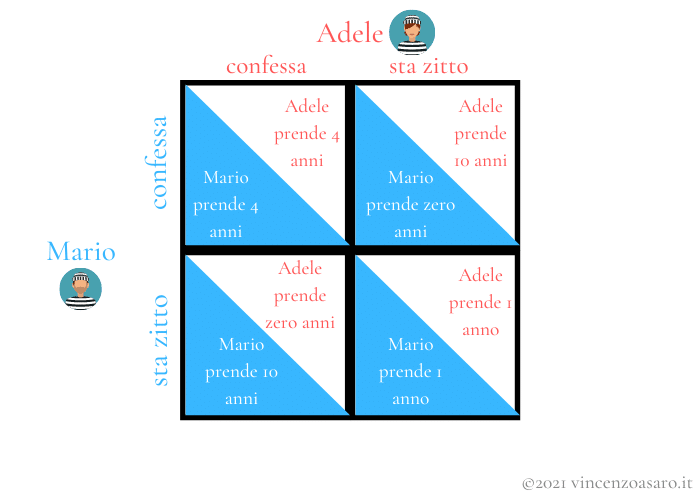
Per osservare le scelte di Mario dobbiamo fare riferimento alle righe. Per osservare le scelte di Adele, invece, dobbiamo fare riferimento alle colonne.
Mario => righe
Adele => colonne
Guardiamo per un attimo le possibili scelte di Mario. Essendo questo un gioco a informazione completa, lui sa che se Adele sta zitta lui può prendere un anno se sta zitto, oppure zero anni se confessa.
Quindi se Adele sta zitta a Mario conviene confessare (prende zero anni, anziché uno).
Se invece Adele confessa, Mario può prendere 10 anni (se sta zitto)oppure 4 anni (se confessa).
Dunque anche se Adele confessa a Mario conviene comunque confessare (prende 4 anni anziché 10).
In questo caso diciamo che confessare è la strategia dominante per Mario.
A Mario conviene sempre confessare.
Se facessimo lo stesso ragionamento per Adele arriveremmo alla stessa conclusione: per Adele la strategia dominante è confessare.
Quindi i due confesseranno, prendendo 4 anni di carcere ciascuno, mentre se avessero tenuto fede alla promessa che si erano fatti di stare zitti avrebbero preso soltanto un anno ciascuno.
Il paradosso del dilemma del prigioniero
Si vede chiaramente nella matrice dei payoff che il risultato migliore per entrambi è quello di far fede alla promessa di non collaborare (prendendo un anno ciascuno).
Tuttavia questa situazione (sta zitto, sta zitta)non è un equilibrio. Da come è strutturato il gioco, l’equilibrio di Nash (quello in cui nessun giocatore vuole modificare la sua strategia)sarà quello meno conveniente per entrambi (confessa, confessa).
Ogni qual volta la strategia dominante è quella inefficiente, e la strategia dominata è quella più efficiente (non confessa, non confessa), ci troviamo di fronte ad un dilemma del prigioniero.
Evitare che si confessi: introdurre minacce credibili
Come abbiamo visto, la strategia dominante per entrambi i giocatori è di confessare.
Tuttavia, se Mario e Adele appartenessero ad un’organizzazione criminale che ha tutto l’interesse a non farli confessare, la matrice dei payoff cambierebbe drasticamente, e l’equilibrio sarebbe diverso.
Se Mario e Adele sapessero che, in caso di confessione, venissero uccisi dagli altri membri dell’organizzazione, la matrice dei payoff sarebbe la seguente:
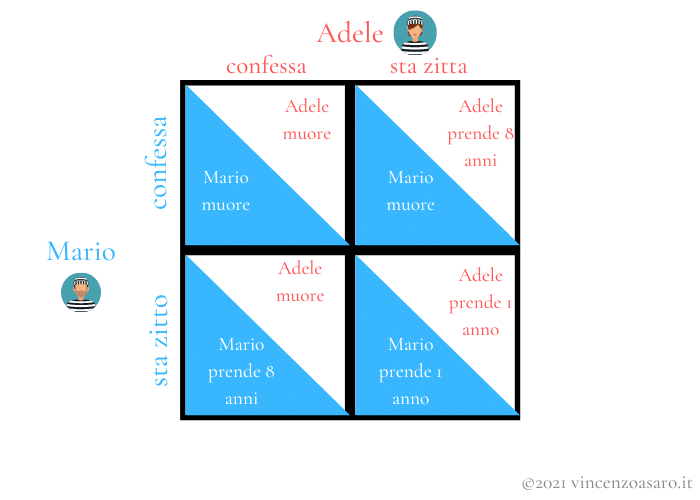
Come vediamo, se c’è una minaccia credibile di morte da parte dell’organizzazione, le strategie dominanti dei due cambiano.
In particolare Mario sa che se Adele confessa, lui ha due scelte: confessare e morire, oppure stare zitto e prendere 8 anni (ma rimanere vivo). Quindi sceglierà certamente di stare zitto.
Se invece Adele sta zitta, Mario sa che confessando muore, mentre se sta zitto prende un anno di carcere. Quindi anche in questo caso a Mario conviene stare zitto.
La strategia dominante di Mario, introducendo una minaccia credibile di morte, diventa stare zitto.
La stessa cosa vale per Adele.
Dunque l’equilibrio di Nash in questo caso sarà (sta zitto, sta zitta).
Notiamo come la minaccia di morte alla fine porta i due all’equilibrio più conveniente per entrambi, quello pareto-efficiente.
Video sul dilemma del prigioniero
Se questo post ti è stato utile, lascia una valutazione qui sotto:




