Esercizi svolti sul vincolo di bilancio: costruire il vincolo di bilancio

In questo post vediamo, passo per passo, due esercizi svolti sul vincolo di bilancio.

Se hai qualsiasi domanda, oppure c’è qualcosa nei tuoi esercizi sul vincolo di bilancio che non capisci, non esitare a lasciare un commento, in modo che anche gli altri lettori possano risponderti!

Un’ulteriore consiglio è di provare prima a svolgere da soli l’esercizio, e soltanto dopo verificare il procedimento guardando agli esercizi svolti sul vincolo di bilancio.

Esercizi svolti sul vincolo di bilancio #1

Gianni ha un reddito di 500 € al mese, che spende interamente per l’acquisto di due beni: pasta (bene 1)e libri (bene 2).
Il prezzo di 1 chilo di pasta è di 2 €, mentre il prezzo medio di un libro è di 10 €.
Scrivete analiticamente il vincolo di bilancio di Gianni e rappresentatelo graficamente.

Per aggiungere un po’ di complessità, dopo aver risolto questa prima parte dell’esercizio, continueremo con altre due domande:

Cosa succede se il reddito di Gianni aumenta a 600 € al mese?
Cosa succede se con il nuovo reddito il prezzo della pasta si riduce ad 1 € al chilo?

Iniziamo con la prima parte dell’esercizio.

Rappresentazione analitica del vincolo di bilancio

Iniziamo con lo scrivere il vincolo di bilancio analiticamente.
In altre parole, partiamo dalla definizione di vincolo di bilancio che abbiamo visto nel post riguardante le scelte del consumatore.

Ricordiamo che in generale il vincolo di bilancio è così definito:

Y = (P₁ • X₁ ) + (P₂ • X₂)

dove:

Y: Reddito del consumatore
P₁ : Prezzo del bene 1
P₂ : Prezzo del bene 2
X₁ : La quantità del bene 1 acquistata
MX₂ : La quantità del bene 2 acquistata

Nel nostro esempio, il bene 1 è la pasta, che costa 2 € al kg.
Il bene 2 sono i libri, che costano in media 10 € per libro.
Il reddito del consumatore (Gianni)è di 500 €.

Quindi possiamo scrivere analiticamente il vincolo di bilancio di Gianni partendo dalla definizione:

500 = (2 X₁ ) + (10 X₂)

Questa formula ci dice semplicemente che Gianni guadagna 500 € al mese (membro di sinistra), e che li spende comprando X₁ chili di pasta al prezzo di 2 €, e X₂ libri, al prezzo di 10 € ciascuno.

Vediamo ora come disegnare il vincolo di bilancio di Gianni partendo da questa definizione.

Rappresentazione grafica del vincolo di bilancio

Osserviamo che matematicamente il vincolo di bilancio non è altro che un’equazione di primo grado, nulla di complicato.

La pendenza è data dal rapporto tra i prezzi (con un meno davanti).

La pendenza del vincolo di bilancio è chiamata MRT (Marginal Rate of Transformation). Un nome complicato per qualcosa di veramente semplice:

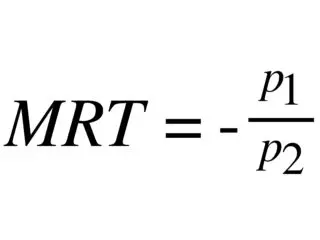
Nel nostro caso, il prezzo del bene 1 (la pasta)è di 2 € al chilo, mentre il prezzo del bene 2 (i libri)è di 10 € a libro.
Quindi non dobbiamo far altro che sostituire questi valori alla formula, ottenendo:

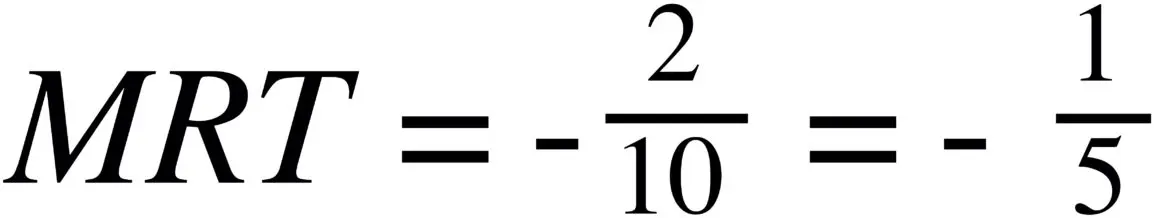
Questa è semplicemente la pendenza del vincolo di bilancio.

Il concetto che sta dietro questi numeri è che per comprare un libro, Gianni deve rinunciare a 5 kg di pasta.

Per disegnare il vincolo, ci servono altri due elementi: le intersezioni con gli assi.

Intersezioni del vincolo di bilancio gli assi

Per trovare le intersezioni con gli assi, ci poniamo due domande:

Domanda #1: quanta pasta può comprare Gianni in un mese, se spende tutto il suo reddito per la pasta (e non compra nessun libro)?

Se Gianni compra solo pasta, la quantità di libri è 0.

Partendo dal vincolo di bilancio di Gianni:

500 = (2 X₁ ) + (10 X₂)

500 = (2 X₁ ) + (10 • 0) = 2 X₁ + 0

X₁ = 500 / 2

X₁ = 250

Quindi, se Gianni comprasse soltanto pasta (e nessun libro)in un mese, potrebbe comprare 250 kg di pasta.

Questa è l’intersezione con l’asse X₁ (l’asse della pasta).

Quando si svolgono gli esercizi, non è necessario fare tutti i calcoli; si può usare la formula breve:

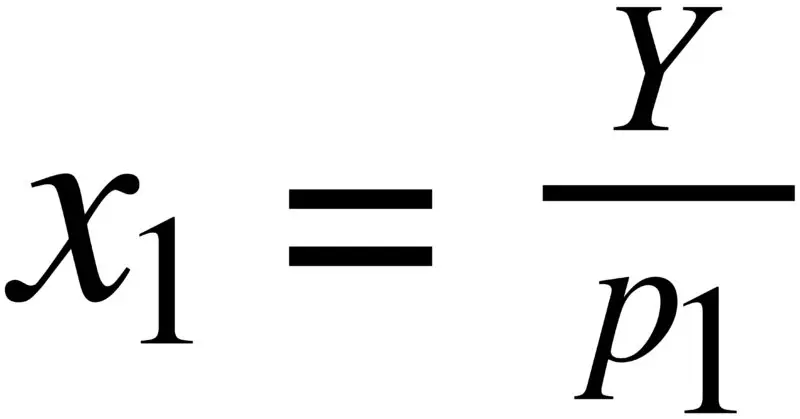
È tuttavia importante conoscere i passaggi che portano a questa formula, sia per comprendere meglio il concetto, sia perché è una exit strategy nel caso in cui dimentichiate la formula.

Dunque sappiamo in quale punto il vincolo di bilancio interseca l’asse X₁.
X₁ = 250

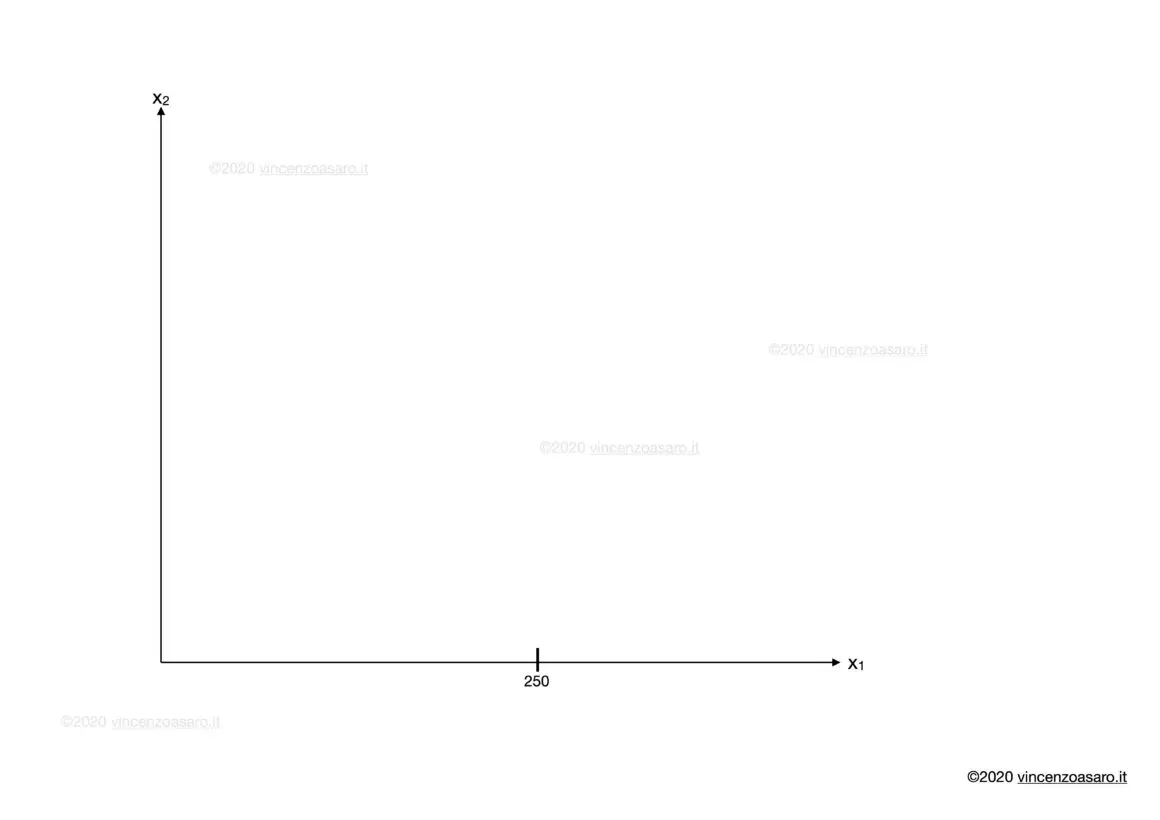
Vediamo evidenziato in basso il punto di intersezione che abbiamo trovato.

Passiamo adesso a trovare l’altro punto di intersezione, ponendoci la seconda domanda.

Domanda #2: quanti libri può comprare Gianni in un mese, se spende tutto il suo reddito per i libri (e non compra pasta)?

Dobbiamo semplicemente ripetere il procedimento, sapendo che in questo caso, la quantità di pasta comprata è zero.

Applichiamo direttamente la formula:

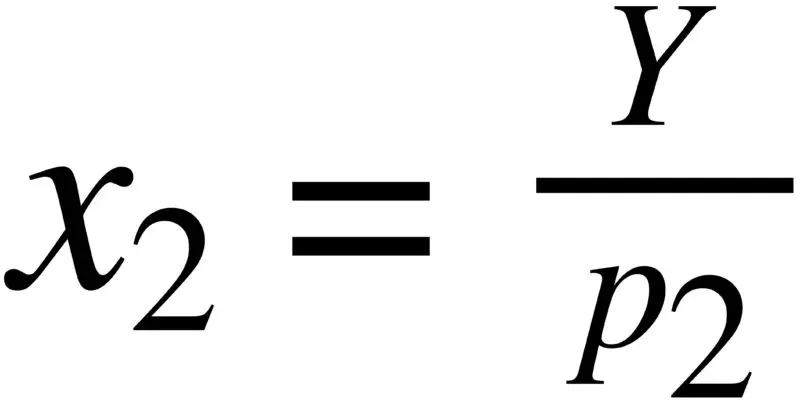
Sappiamo che il reddito (Y)è 500, e che il prezzo dei libri è di 10 € al libro, quindi:

X₂ = 500 / 10 = 50

Quindi, se Gianni comprasse soltanto libri, potrebbe comprarne 50 al mese.
Aggiungiamo questa informazione nel grafico:

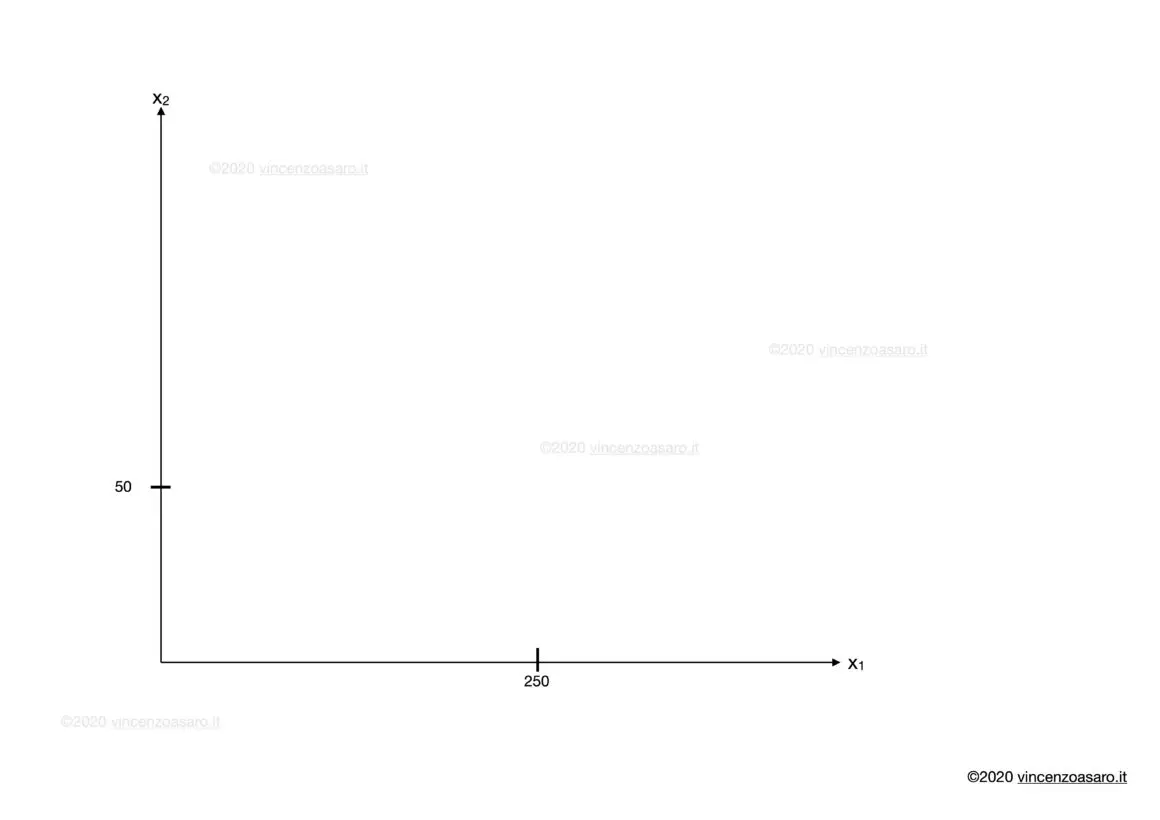
Disegniamo il vincolo di bilancio

Adesso conosciamo la pendenza del vincolo di bilancio, e conosciamo le intersezioni con i due assi (sarebbero bastate le intersezioni per disegnare il vincolo di bilancio, dal momento che per due punti passa una sola retta).

Possiamo quindi rappresentare graficamente il vincolo di bilancio:

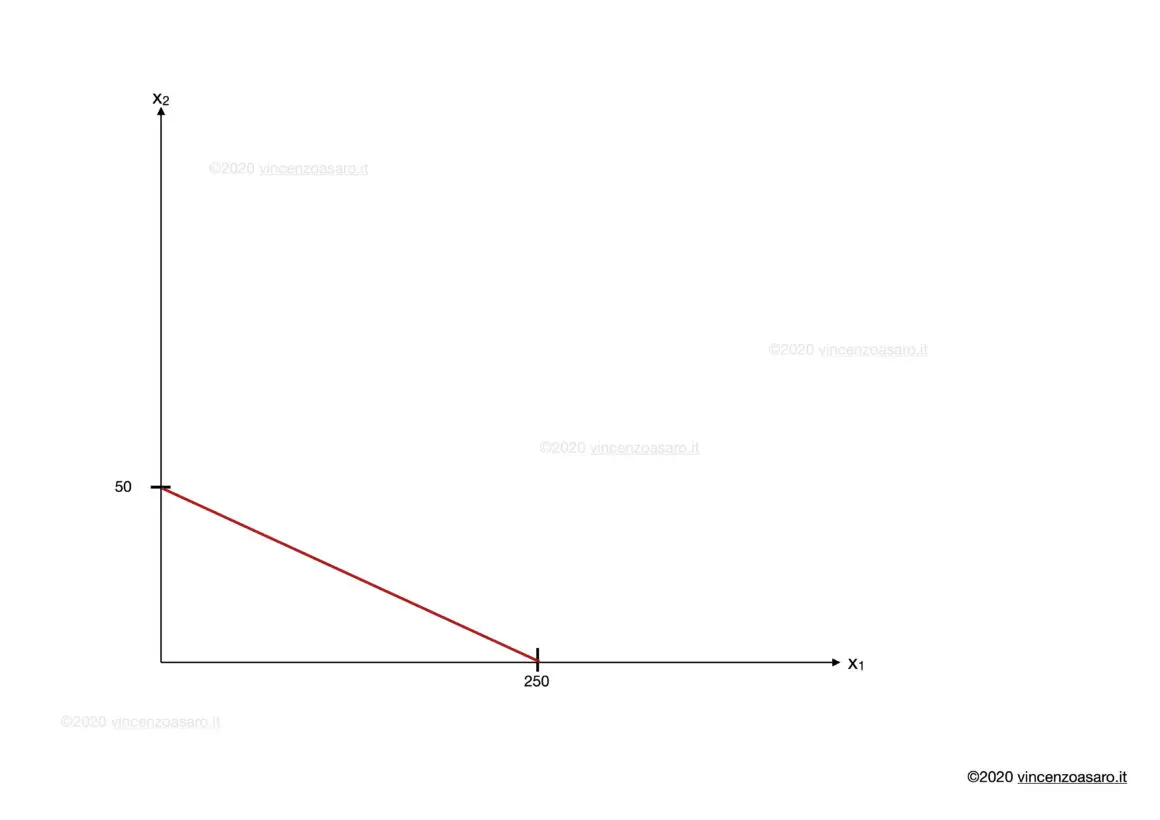
Questo completa la prima parte dell’esercizio.

Gli esercizi svolti sul vincolo di bilancio, tuttavia, spesso includono delle variazioni.
Per questo motivo, analizziamo adesso un paio di casi in cui aggiungiamo un po’ di complessità all’esercizio corrente.

Il reddito aumenta

Cosa succede se il reddito di Gianni aumenta a 600 € al mese?

Se il reddito di Gianni aumenta, tutte le formule precedenti si modificano.

Ciò che cambia sono le intersezioni con gli assi. In particolare le nuove intersezioni sono:

In altre parole, il nuovo vincolo di bilancio è parallelo a quello precedente (ha la stessa pendenza, i prezzi relativi dei due beni sono uguali!).

Tuttavia è spostato verso destra (Gianni può comprare maggiori quantità di entrambi i prodotti, perché è più ricco).

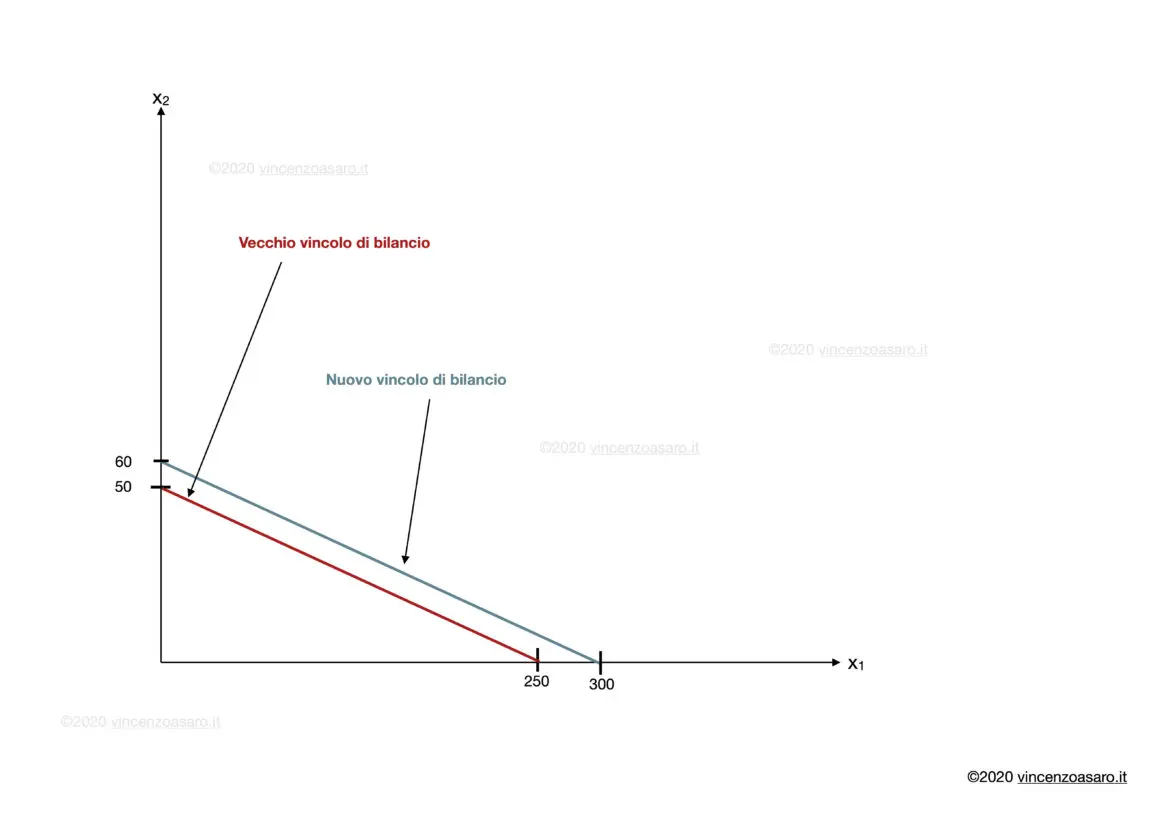
I due vincoli di bilancio (vecchio e nuovo)hanno la stessa pendenza!

Il prezzo di un bene cambia

Cosa succede se con il nuovo reddito il prezzo della pasta si riduce ad 1 € al chilo?

Aggiungiamo un’ulteriore livello di complessità. Abbiamo appena visto come è cambiato il vincolo di bilancio a seguito di un aumento del reddito.
Il vincolo ha la stessa pendenza di quello precedente(perché i prezzi relativi dei due beni non sono cambiati), ma è traslato verso destra.

Adesso vogliamo sapere cosa succede se il prezzo della pasta diminuisce. Da 2 € al chilo, passa ad 1 € al chilo.

Dunque adesso il nuovo vincolo di bilancio non è parallelo al precedente, perché il coefficiente angolare è cambiato.

Mentre prima rinunciando ad un libro Gianni poteva comprare 5 kg di pasta, adesso rinunciando sempre ad un solo libro, può comprare 10 kg di pasta.

Sono cambiate, ovviamente, anche le intersezioni con gli assi. Le nuove intersezioni sono:

Notiamo che l’intersezione con l’asse dei libri NON è cambiata (perché il prezzo dei libri è rimasto uguale).

È cambiata l’intersezione con l’asse della pasta.

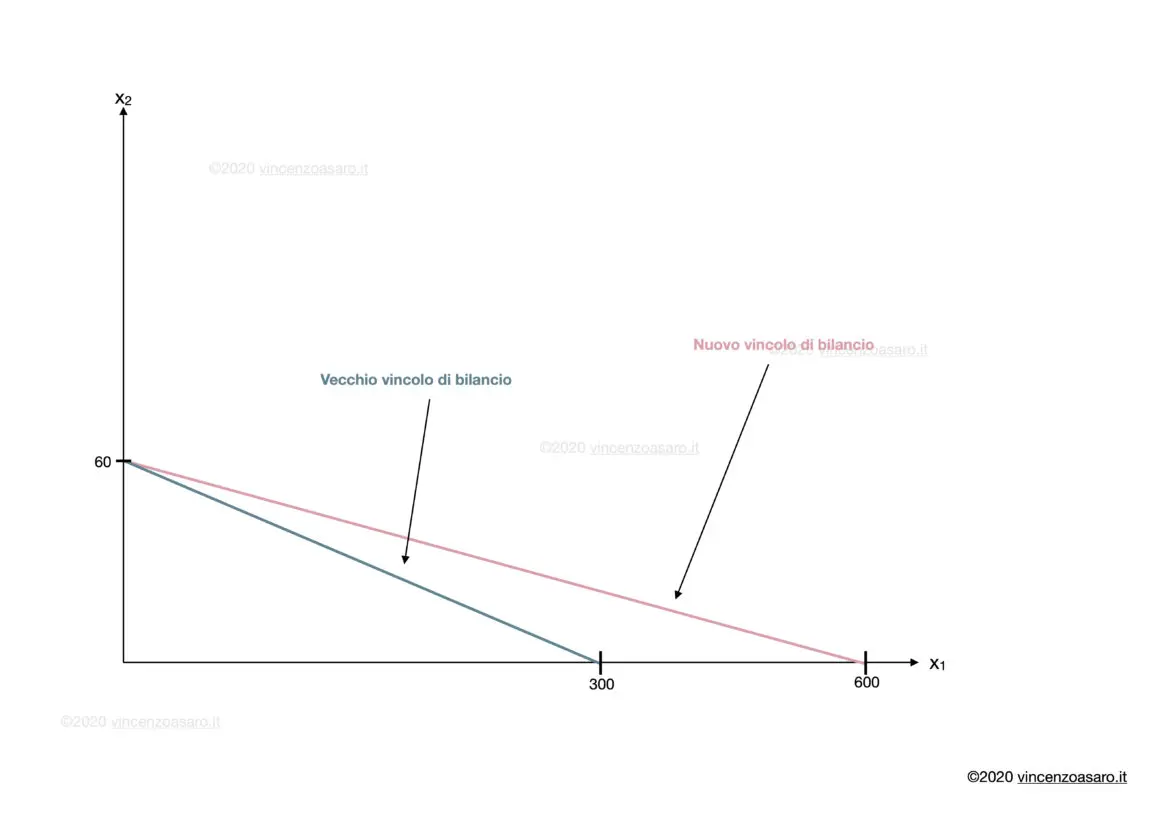
Questo conclude il primo esercizio svolto sul vincolo di bilancio.

Adesso passiamo alla risoluzione di un altro esercizio.

Esercizi svolti sul vincolo di bilancio #2

Massimo guadagna un reddito di 1.000 € al mese, che spende interamente per l’acquisto del bene 1 (acquisto di videogiochi)e del bene 2 (ingressi al cinema).
Il prezzo medio di un videogioco (P₁) è di 10 € ciascuno, mentre un ingresso al cinema (P₂) costa 8 €.
Scrivere analiticamente e disegnare il vincolo di bilancio.

Il procedimento di risoluzione è uguale al precedente, quindi passiamo direttamente a calcolare le soluzioni, senza soffermarci troppo sui passaggi. Come riferimento puoi sempre guardare all’esercizio svolto #1.

Partendo dalla definizione di vincolo di bilancio, possiamo scrivere il vincolo di bilancio di Massimo analiticamente nel modo seguente:

1.000 = 10 X₁ + 8 X₂

Da qui, possiamo determinare immediatamente le intersezioni con gli assi.

Infine determiniamo la pendenza del vincolo di bilancio, che ricordiamo essere data dal rapporto tra i due prezzi ed il segno meno (lo si può evincere facilmente con pochi passaggi algebrici).

MRT = – 10/8 = – 5/4 = – 1,25

Dunque la pendenza è – 1,25

Possiamo passare a disegnare il vincolo di bilancio, con i dati che abbiamo:

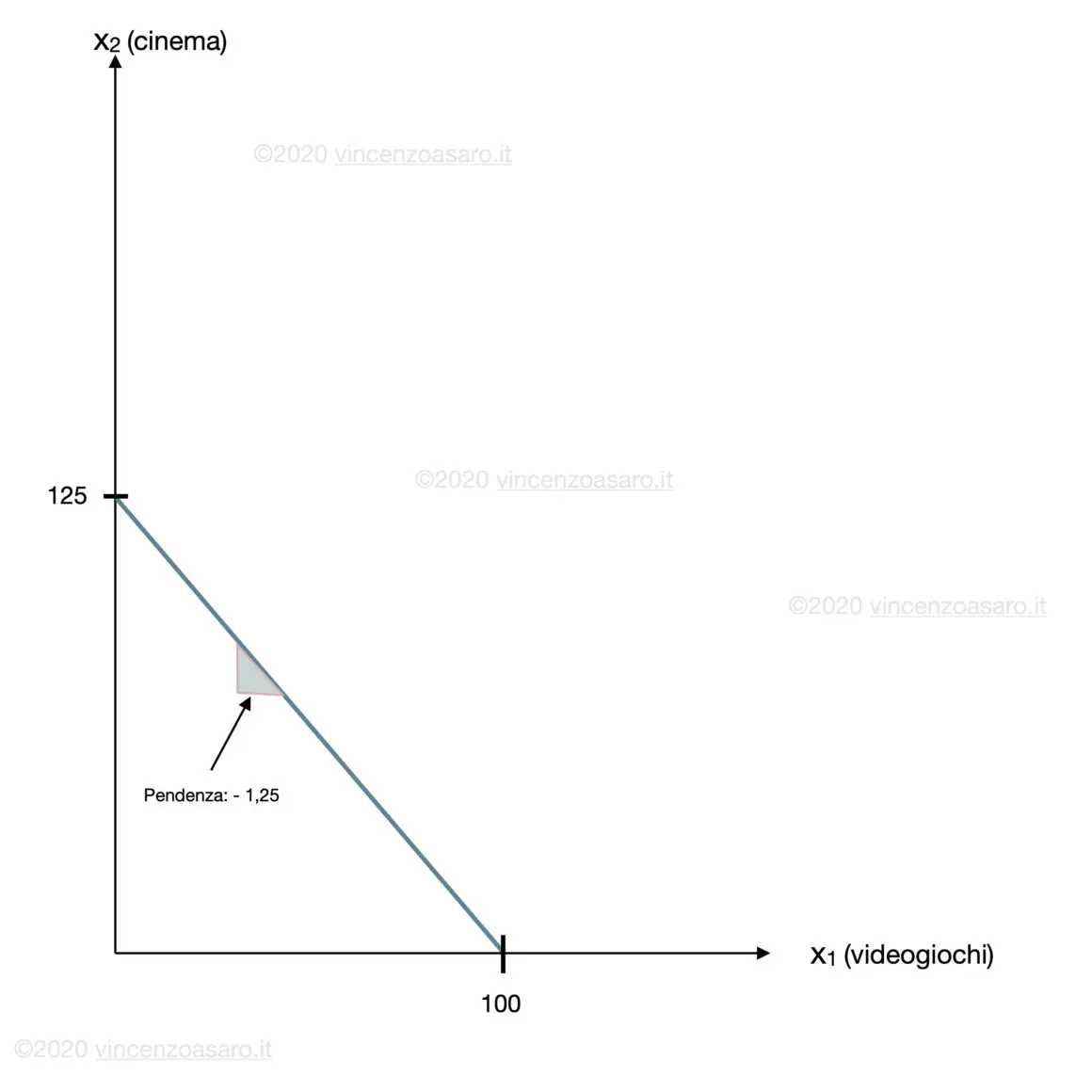
Questo conclude questo secondo esercizio più breve.

Video esercizio svolti sul vincolo di bilancio

Ecco un breve video, in cui vediamo passo per passo alcuni esercizi svolti sul vincolo di bilancio, per fare pratica.

Altre risorse

Elenco qui alcune risorse selezionate tra quelle in rete, che contengono esercizi svolti sul vincolo di bilancio, e che potete consultare per esercitarvi ulteriormente:

• https://www.giappichelli.it/media/catalog/product/excerpt/9788892109308.pdf
• http://www.dse.univr.it/documenti/OccorrenzaIns/matdid/matdid786845.pdf
• https://www.unirc.it/documentazione/materiale_didattico/600_2009_206_4592.pdf

Per qualsiasi domanda o suggerimento, come sempre, non esitare a contattarmi o a scrivere il tuo commento in basso!