In questo post approfondiremo la relazione tra la funzione di produzione e la forma delle curve di costo nel breve periodo.
Sarebbe quindi opportuno, prima di leggere questo post, rivedere i post relativi alle curve di costo e alla funzione di produzione cliccando sui pulsanti qui sotto:
Faremo un breve richiamo sulla funzione di produzione di breve periodo e sui costi nel breve periodo per poi parlare della relazione tra i costi e la produzione. Più in particolare parleremo della relazione tra il prodotto marginale del lavoro e il costo marginale, e della relazione tra il prodotto medio del lavoro ed il costo variabile medio.
Richiamo sulla funzione di produzione di breve periodo
Nel breve periodo un input (tipicamente il capitale, K)è fisso – e dunque lo indichiamo nella funzione di produzione con una barretta sopra – mentre un input (tipicamente il lavoro, L)è variabile.
La funzione di produzione di breve periodo sarà la seguente:
q = f(L,K̅)
Introduciamo alcuni concetti:
- Prodotto totale (q): quantità totale prodotta dati i fattori produttivi.
- Prodotto marginale del lavoro (MPL) [ Marginal product of labour]
Indica la variazione di prodotto totale derivante dall’utilizzo di un’unità aggiuntiva di lavoro. - Prodotto medio del lavoro (APL) [Average product of labour]
È il rapporto tra la produzione totale (q)e il lavoro totale (L)impiegato per realizzarlo.
In simboli:
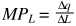
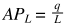
Richiamo sui costi di breve periodo
Definiamo:
- Costo marginale (MC – Marginal Cost)
MC = ∆C / ∆q
Ma il costo totale (C)è uguale al costo variabile nel breve periodo (VC), quindi:
MC = ∆VC / ∆q - Costo variabile medio (AVC – Average Variable Cost)
AVC = VC/q
Relazione tra costi e produzione
Avendo brevemente riassunto i concetti di produzione e costo sopra citati (che sono approfonditi nei relativi post, che potete trovare all’inizio di questo articolo, cliccando sui pulsanti dedicati) passiamo ad osservare la relazione che intercorre tra i costi e la produzione nel breve periodo.
Relazione tra prodotto marginale del lavoro e costo marginale
w è il costo unitario (ovvero il costo orario)del lavoro.
Nel breve periodo il costo del capitale è fisso (perché il capitale, K, è un input fisso).
L’unico costo variabile è quello del lavoro.
quindi il costo variabile (VC) è il seguente:
VC = wL
Come abbiamo già visto, il costo marginale è:
MC = ∆VC/∆q
Ma sappiamo che nel breve periodo, essendo l’unico input variabile il lavoro: VC = wL
Di conseguenza:
MC = w∆L / ∆q = w*(∆L/∆q) = w/(∆q/∆L)
Osserviamo che MC = w / (∆q/∆L)
Ma abbiamo già visto che ∆q/∆L = MPL
Quindi in definitiva, nel breve periodo il costo marginale (MC) è uguale al costo orario del lavoro (w) diviso il prodotto marginale del lavoro (MPL)
MC = w/MPL
Relazione tra prodotto medio del lavoro e costo variabile medio
Come abbiamo visto, il costo variabile medio (AVC)è dato dal costo variabile (VC) diviso la quantità di output (q):
AVC = VC/q
Ma abbiamo già visto che il costo variabile (VC)nel breve periodo coincide con il costo del lavoro, dato dal costo orario del lavoro (w)moltiplicato per le ore lavorate (L):
VC = wL
Dunque, possiamo scrivere, sostituendo wL a VC nella prima equazione, che:
AVC = wL/q
Che riorganizzando i termini è uguale a:
AVC = w*(L/q)
Che a sua volta, portando il reciproco di L/q al denominatore, è uguale a:
AVC = w/ (q/L)
Fermiamoci un attimo! C’è qualcosa in questa equazione che abbiamo già visto:
q/L = APL
La quantità di output (q)diviso la quantità di lavoro (L) è il prodotto medio del lavoro (APL).
Quindi, in definitiva:
AVC = w/APL
Riassunto
In breve, abbiamo osservato che:
- Il costo marginale (MC)è dato dal costo unitario (o orario)del lavoro, cioè w, diviso per la produttività marginale del lavoro (MPL).
Se lavoro un’ora in più, quanto mi costerà quest’ora di lavoro (numeratore)? E quanto prodotto aggiuntivo mi da (denominatore)? - Il costo variabile medio (AVC)è dato dal costo orario del lavoro (w)diviso il prodotto medio del lavoro (APL).
Quanto mi costa un’ora di lavoro (numeratore)? Quanto si produce mediamente in un’ora (denominatore)?




la pagina risulta deformata
Io la vedo correttamente dal mio browser. Prova a cancellare la cache e i cookies o usare un altro browser.