Questa è una spiegazione dei costi in microeconomia semplice e breve.
C’è un post più approfondito dedicato all’argomento, che potete trovare cliccando sul pulsante qui sotto:
Se dovessi avere qualsiasi domanda non esitare a contattarmi, oppure a lasciare un commento.
Adesso passiamo al nostro argomento: i costi in microeconomia in breve.
Quali costi prendiamo in considerazione?
I costi che prendiamo in considerazione in microeconomia sono sia quelli impliciti che quelli espliciti.
In particolare, gli economisti prendono in considerazione il costo opportunità.
I sunk costs non devono influire sulle decisioni dell’impresa.
Anche il capitale viene calcolato al valore opportunità (non al costo storico).
I costi nel breve periodo
Costo totale
Nel breve periodo, per definizione, almeno uno degli input non può essere adeguato. Quindi un input è variabile (tipicamente il lavoro – L)e un input è fisso (tipicamente il capitale – K).
Dunque, nel breve periodo l’impresa ha dei costi fissi (dei costi, cioè, che non variano al variare della quantità di output).
Costo totale = Costo variabile + Costo Fisso
Lo indicheremo con:
C = VC + F
Graficamente si rappresenta così:
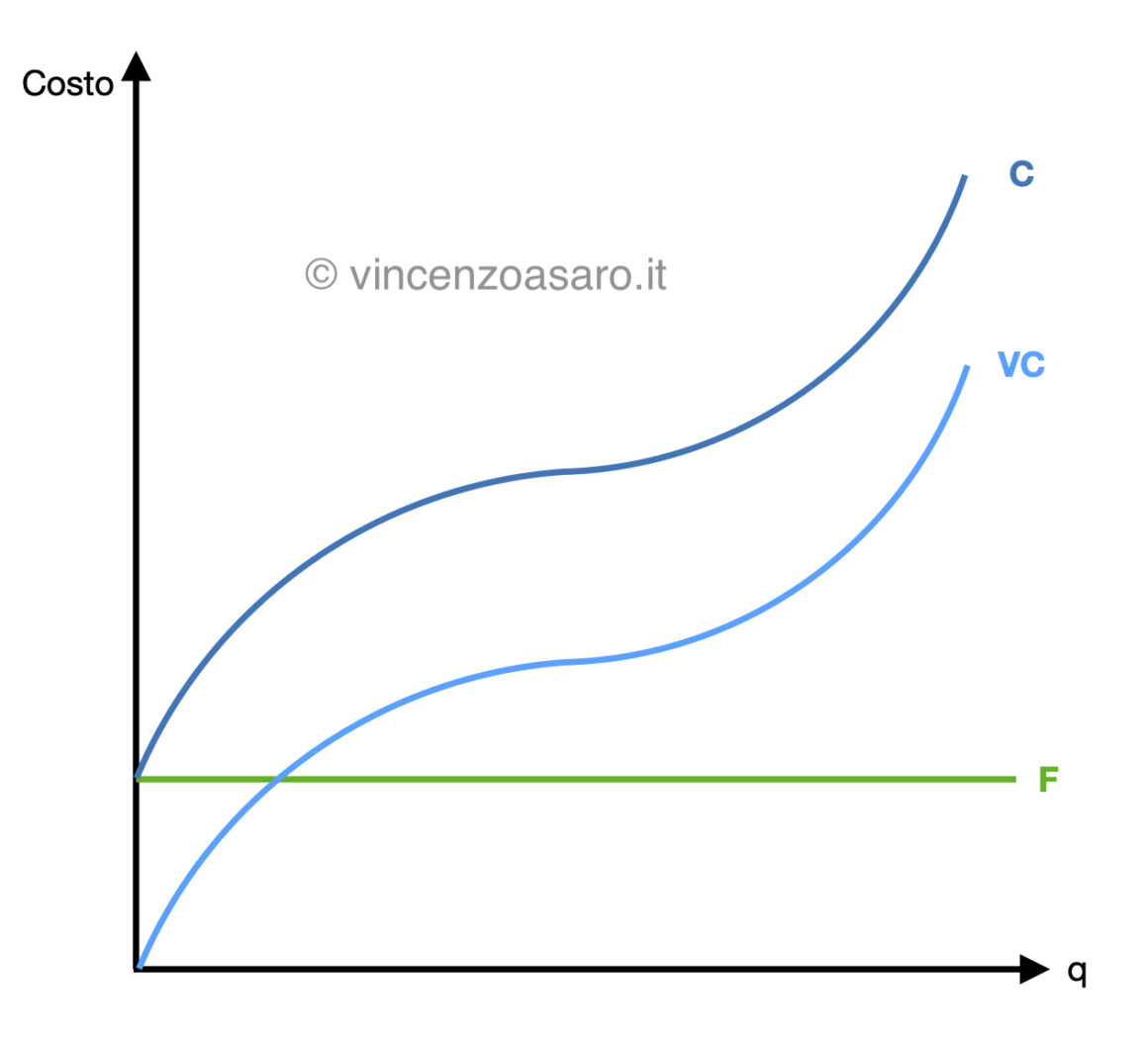
Per la spiegazione completa di come si costruiscano queste curve di costo, rimandiamo sempre al post più approfondito, precedentemente citato.
Costi medi e marginali
Il costo marginale
Definiamo costo marginale (MC – Marginal Cost)la variazione del costo per un’unità in più di output.
Esempio: se produco un kg di riso in più, quanto mi costa quest’ultimo kg prodotto?
MC = ∆C/∆q
Il costo medio
Il costo medio (AC – Average Cost)è la somma dei costi variabili medi e dei costi fissi medi.
AC = AVC + AFC
Il costo variabile medio (AVC – Average Variable Cost)è la divisione dei costi variabili per la quantità prodotta.
AVC = VC / q
Il costo fisso medio (AFC – Average Fixed Cost)è la divisione dei costi fissi per la quantità prodotta.
AFC = F/q
Osserviamo adesso come si rappresentano graficamente tutte queste definizioni di costo.
Rappresentazione grafica dei costi medi e marginali
Graficamente, i costi medi e marginali sono rappresentati come segue:
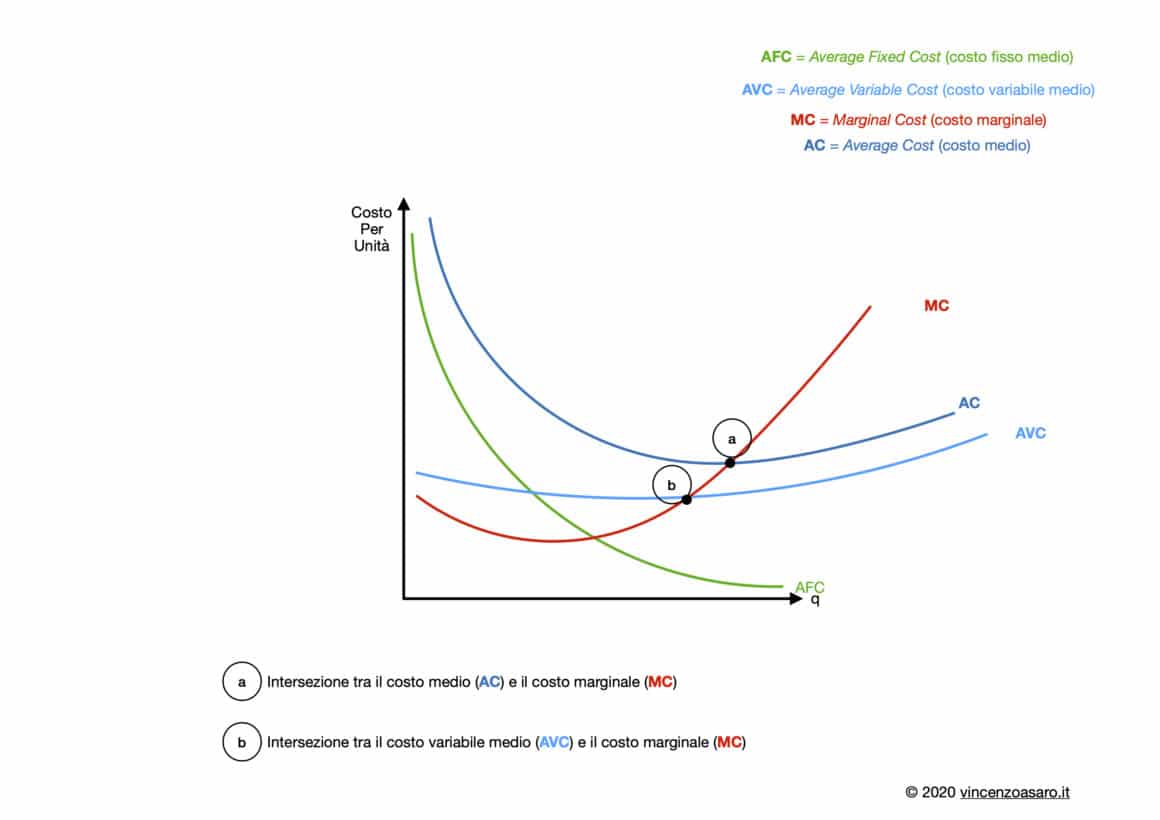
Per i dettagli sulle varie intersezioni e sulle forme delle curve di costo, rimandiamo sempre al post completo sui costi.
C’è anche un video sul nostro canale YouTube sulla relazione tra la curva di costo marginale e la curva di costo medio.
Relazioni tra i costi totali ed i costi medi e marginali
Mettiamo adesso insieme i grafici dei costi totali, e dei costi medi e marginali visti finora, per osservare le relazioni che intercorrono tra essi.
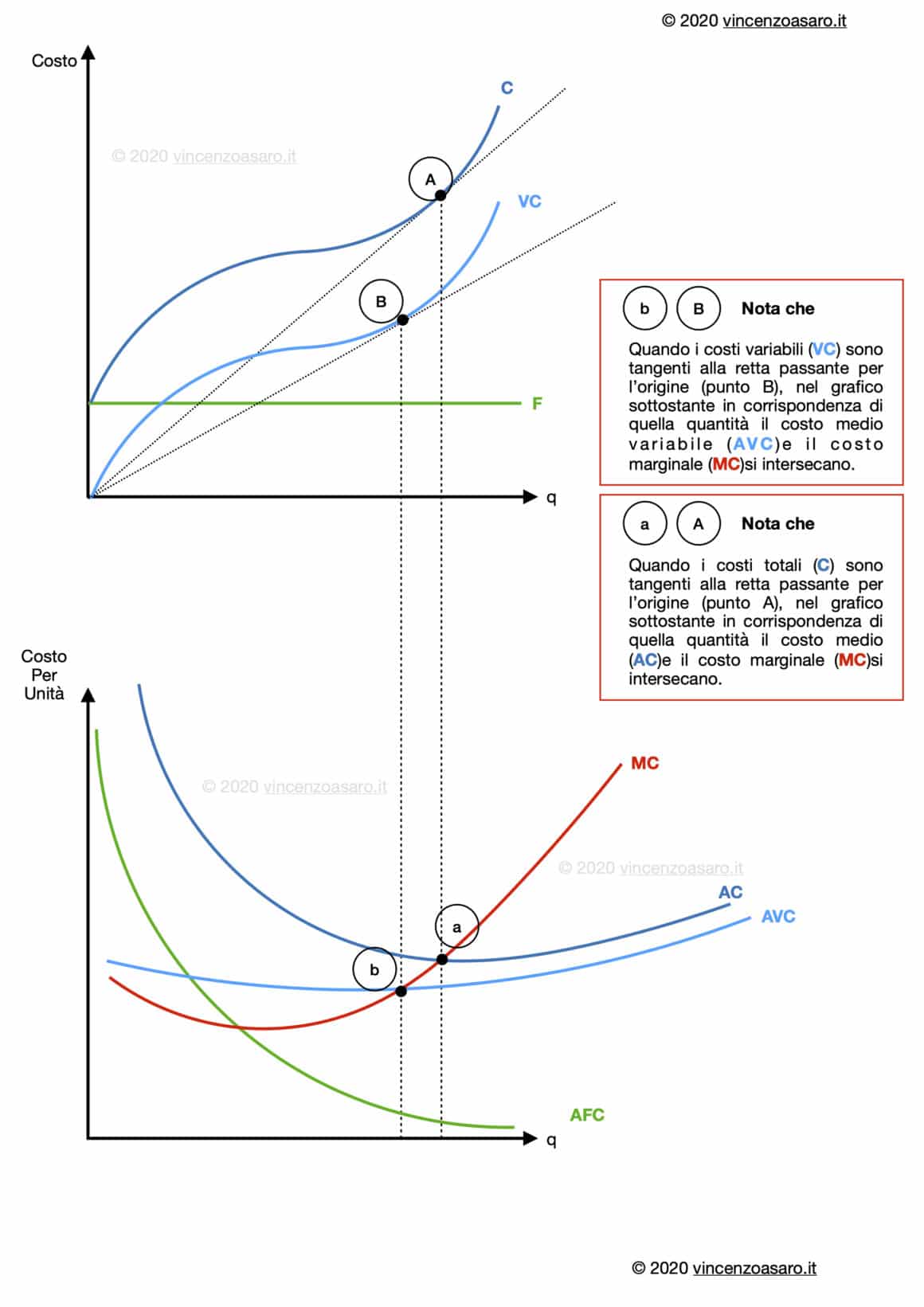
Le relazioni dettagliate sono spiegate approfonditamente nel post più volte citato.
In questa sede ci limitiamo ad osservare che:
- Quando MC si interseca con AVC (punto b del grafico di sotto), AVC è nel suo punto di minimo. Prima di b decresce, dopo di b cresce.
- Quando AC tocca MC (nel punto a del grafico di sotto), AC è nel suo punto minimo. Prima di a decresce, dopo cresce.
- AFC è sempre decrescente, perché i costi fissi (F)sono spalmati su una quantità (q)maggiore.
- La distanza tra AC e AVC (che è costituita da AFC. Ricorda che AC = AVC + AFC)si va assottigliando.
Il motivo è che i costi fissi medi (AFC)vanno pesando sempre meno.
Passiamo adesso ai costi nel lungo periodo.
I costi nel lungo periodo
Nel lungo periodo, per definizione, l’impresa non ha input fissi.
Tutti gli input sono variabili, e non ci sono costi fissi (F = 0).
Dunque l’impresa dovrà pagare soltanto per gli input variabili, che sono capitale (K)e lavoro (L).
C = wL + rK
w è il costo orario del lavoro, e r è il costo orario del capitale.
Il costo è uguale al costo orario del lavoro (w)per le ore lavorate (L) più il costo orario del capitale (r)per le ore di utilizzo del capitale (K).
La linea di isocosto
Per rappresentare i costi nel lungo periodo si usa la linea di isocosto.
Una linea di isocosto rappresenta un costo costante lungo di essa, con diverse combinazioni di lavoro e capitale.
C̅= wL + rK
Il trattino sopra la C indica che il costo è costante lungo la linea.
Risolvendo in funzione di K, otterremo:
Per rappresentare i costi nel lungo periodo si usa la linea di isocosto.
Una linea di isocosto rappresenta un costo costante lungo di essa, con diverse combinazioni di lavoro e capitale.
C̅= wL + rK
Il trattino sopra la C indica che il costo è costante lungo la linea.
Risolvendo in funzione di K, otterremo:
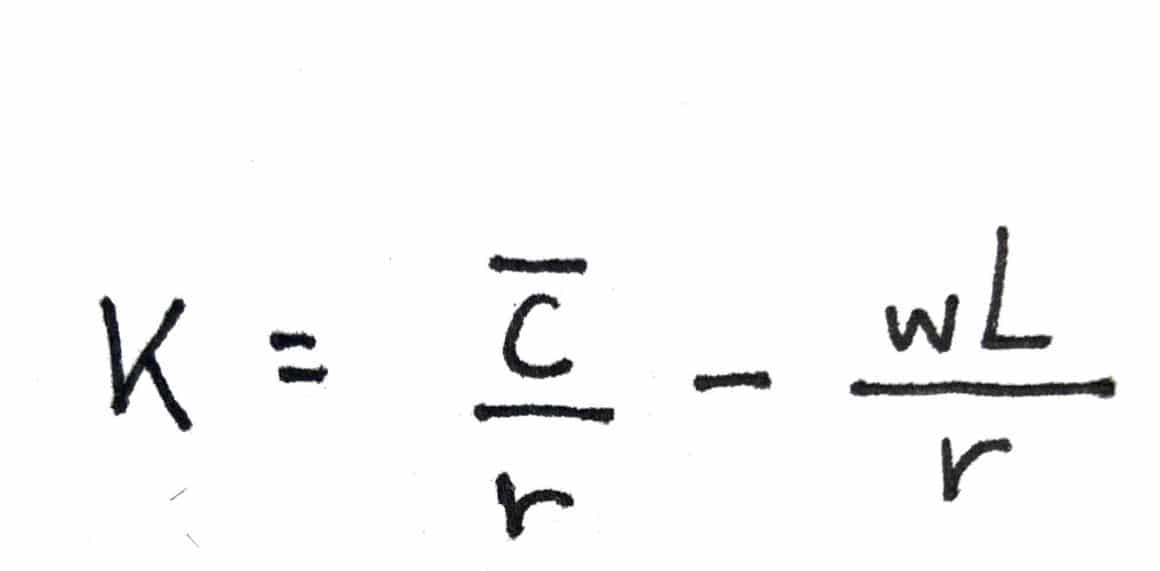
Che è uguale a:
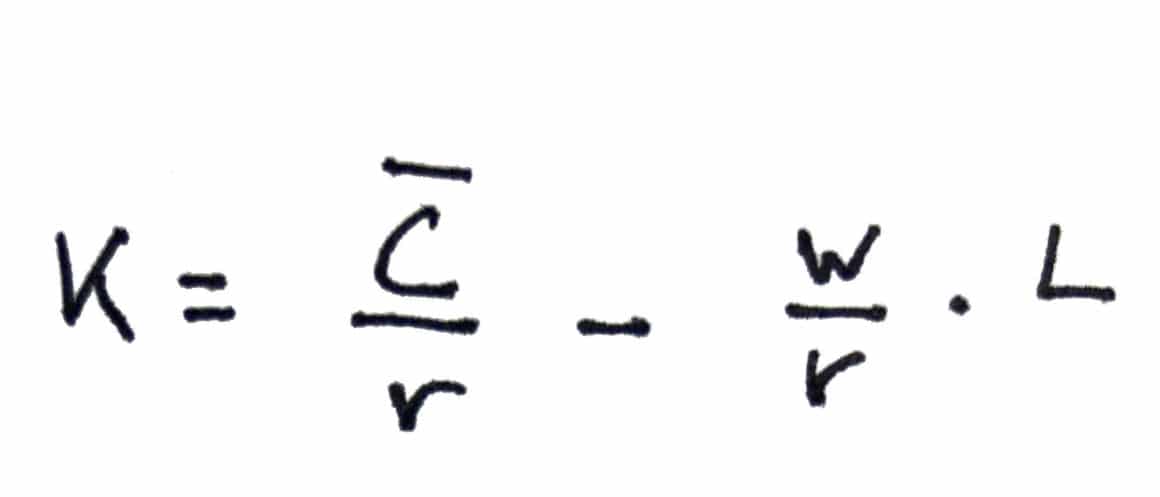
Scrivere l’equazione di un isocosto in funzione di K ci serve per disegnare la linea di isocosto.
Rappresentazione grafica dell’isocosto
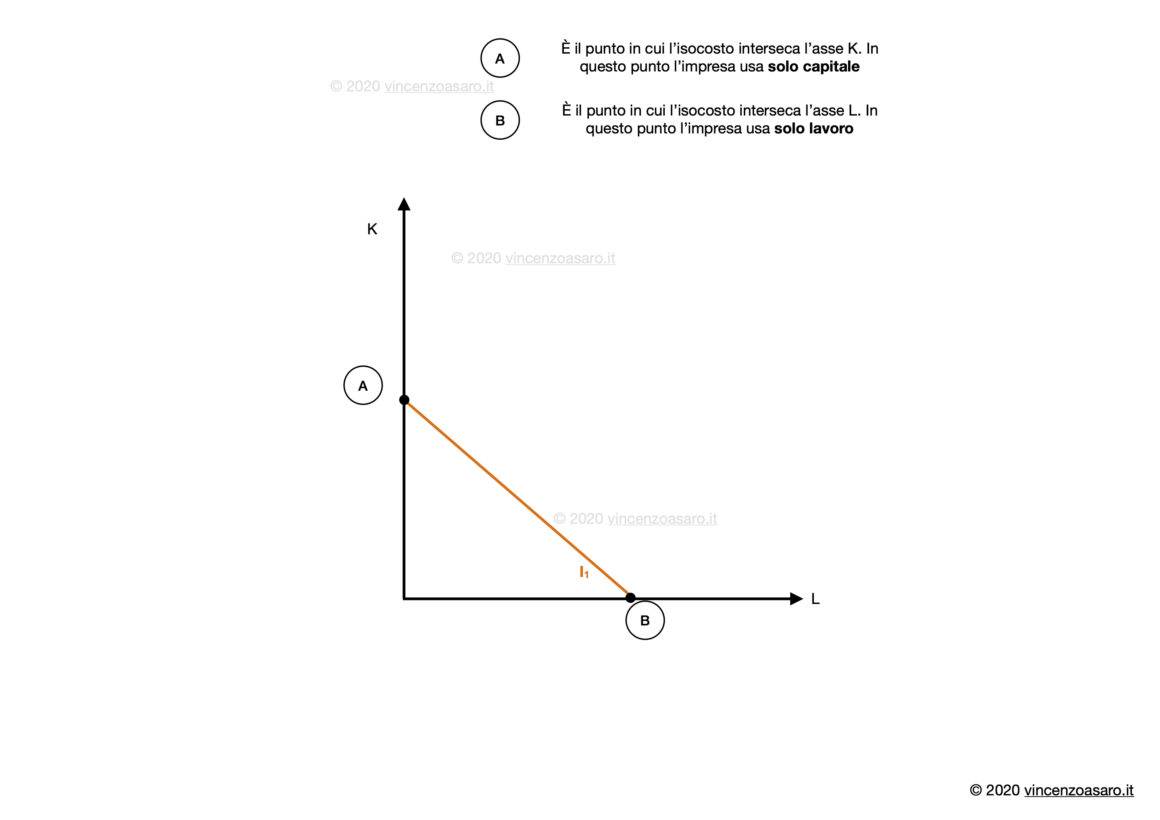
Ovviamente ci possono essere diverse linee di isocosto.
Ogni linea ha un dato livello di costo lungo se stessa.
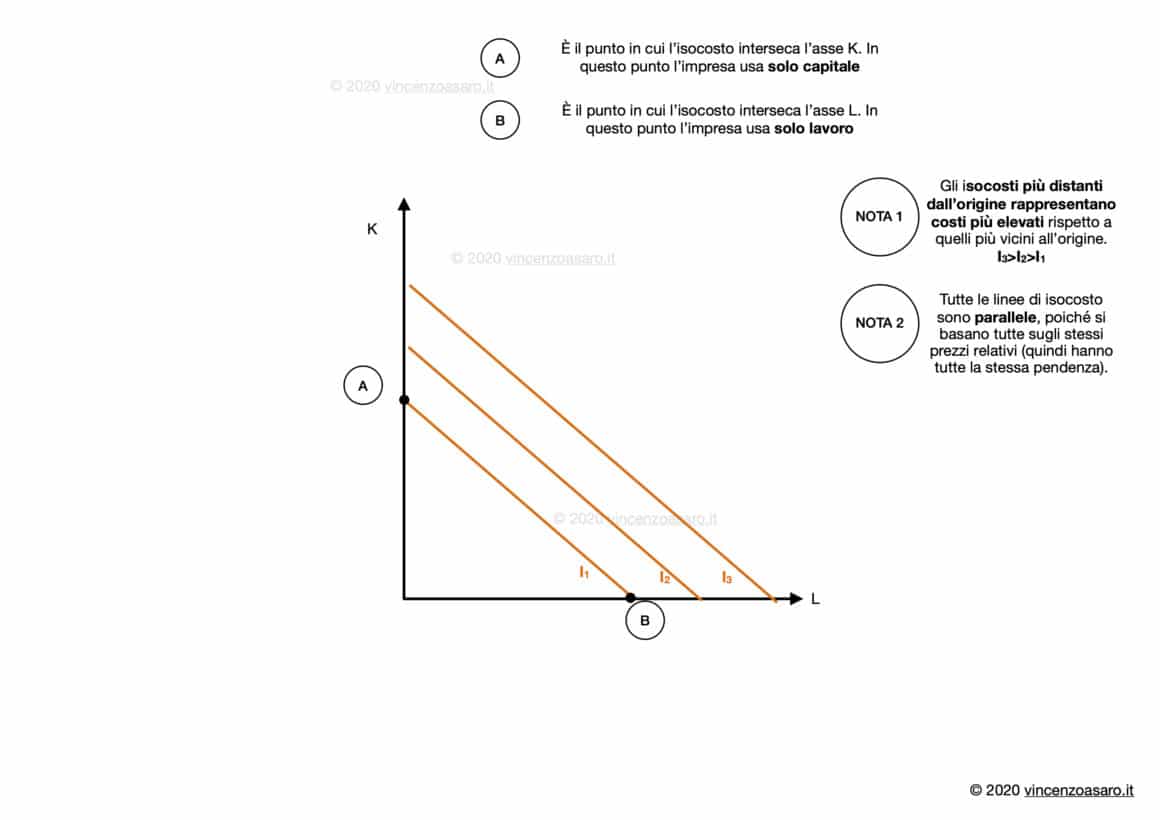
Notiamo che:
- Gli isocosti più distanti dall’origine rappresentano costi più elevati rispetto a quelli più vicini all’origine.
Ovviamente, più un isocosto è distante dall’origine, maggiori saranno le quantità di lavoro e capitale impiegate. - Tutte le linee di isocosto sono parallele.
Poiché tutte le linee di isocosto si basano sugli stessi prezzi relativi (del lavoro e del capitale), esse hanno tutte la stessa pendenza, dunque sono parallele.
Ribadisco per l’ultima volta che questo è un post sintetico, in cui non ci si sofferma su ogni curva o formula e sui vari concetti. È presente un post esteso riguardante i costi in microeconomia, che potete trovare cliccando sul pulsante qui sotto: